一. Predicting Movie Ratings
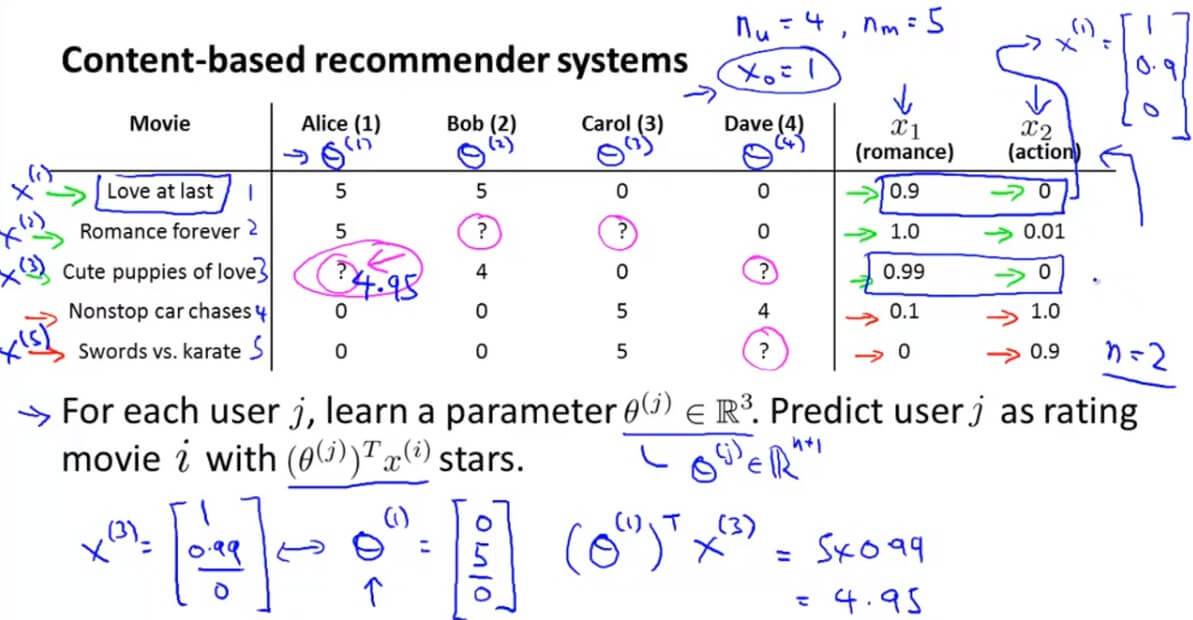
以预测第3部电影第1个用户可能评的分数为例子。
首先我们用 $x_1$ 表示爱情浪漫电影类型, $x_2$ 表示动作片类型。上图左表右侧则为每部电影对于这两个分类的相关程度。我们默认 $x_0=1$ 。则第一部电影与两个类型的相关程度可以这样表示:
$x^{(3)}=\left[ \begin{array}{ccc}1 \\ 0.99 \\ 0 \\ \end{array} \right]$ ,然后用 $\theta^{(j)}$ 表示第 j 个用户对于该种类电影的评分。这里我们假设已经知道(详情下面再讲) $\theta^{(1)}=\left[ \begin{array}{ccc}0 \\ 5 \\ 0 \end{array} \right]$ ,那么我们用 $(\theta^{(j)})^Tx^{(i)}$ 即可计算出测第3部电影第1个用户可能评的分数。这里计算出是4.95。
1. 目标优化
为了对用户 j 打分状况作出最精确的预测,我们需要:
计算出所有的 $\theta$ 为:
与前面所学线性回归内容的思路一致,为了计算出 $J(\theta^{(1)},\cdots,\theta^{(n_u)})$,使用梯度下降法来更新参数:
更新偏置(插值):
更新权重:
二. Collaborative Filtering 协同过滤
前提是我们知道了 $\theta^{(j)}$ 也就是每个用户对于各个电影类型的喜爱程度。那么我们就可以根据各个用户对各部电影的评分= $(\theta^{(j)})^Tx^{(i)}$ 反推出 $x^{(i)}$ 。
1. 目标优化
当用户给出他们喜欢的类型,即 $\theta^{(1)},\cdots,\theta^{(n_u)}$ ,我们可以由下列式子得出 $x^{(i)}$ :
可出所有的 x 则为:
只要我们得到 $\theta$ 或者 x ,都能互相推导出来。
协同过滤算法基本思想就是当我们得到其中一个数据的时候,我们推导出另一个,然后根据推导出来的再推导回去进行优化,优化后再继续推导继续优化,如此循环协同推导。
2. 协同过滤的目标优化
- 推测用户喜好:给定$x^{(1)},\cdots,x^{(n_m)}$ ,估计$\theta^{(1)},\cdots,\theta^{(n_\mu)}$ :
- 推测商品内容:给定$\theta^{(1)},\cdots,\theta^{(n_\mu)}$ ,估计$x^{(1)},\cdots,x^{(n_m)}$ :
- 协同过滤:同时优化$x^{(1)},\cdots,x^{(n_m)}$ ,估计$\theta^{(1)},\cdots,\theta^{(n_\mu)}$:
即:
因为正则化的原因在这里面不再有之前的 $x_0=1$,$\theta_0=0$ 。
3. 协同过滤算法的步骤为:
- 随机初始化$x^{(1)},\cdots,x^{(n_m)},\theta^{(1)},\cdots,\theta^{(n_\mu)} $为一些较小值,与神经网络的参数初始化类似,为避免系统陷入僵死状态,不使用 0 值初始化。
- 通过梯度下降的算法计算出$J(x^{(1)},\cdots,x^{(n_m)},\theta^{(1)},\cdots,\theta^{(n_\mu)})$,参数更新式为:
- 如果用户的偏好向量为$\theta$,而商品的特征向量为 x ,则可以预测用户评价为 $\theta^Tx$ 。
因为协同过滤算法 $\theta$ 和 x 相互影响,因此,二者都没必要使用偏置 $\theta_0$ 和 $x_0$,即,$x \in \mathbb{R}^n$、 $\theta \in \mathbb{R}^n$ 。
三. Low Rank Matrix Factorization 低秩矩阵分解
1. 向量化
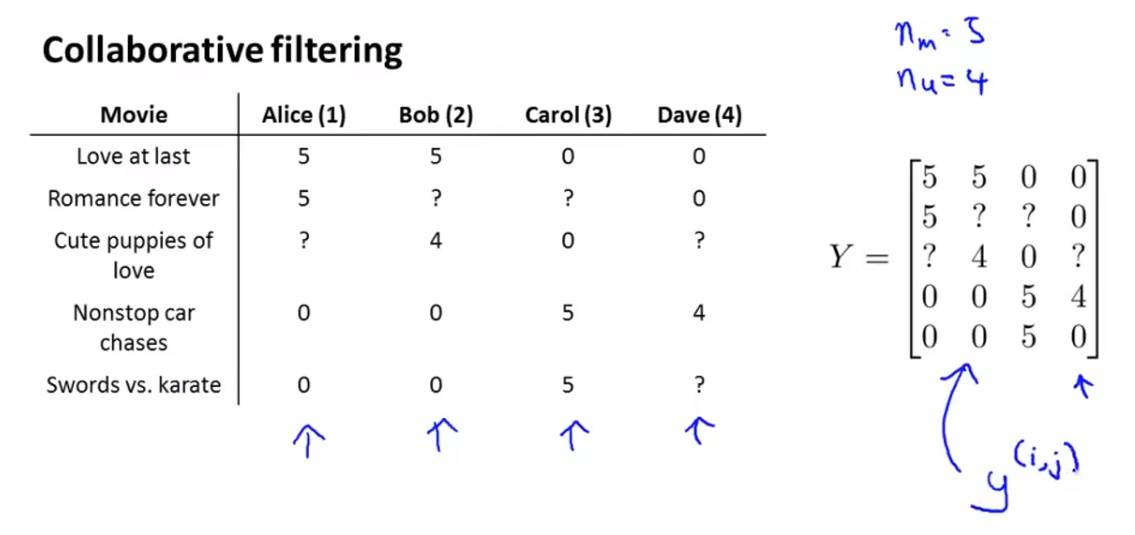
还是以电影评分为例子。首先我们将用户的评分写成一个矩阵 Y 。
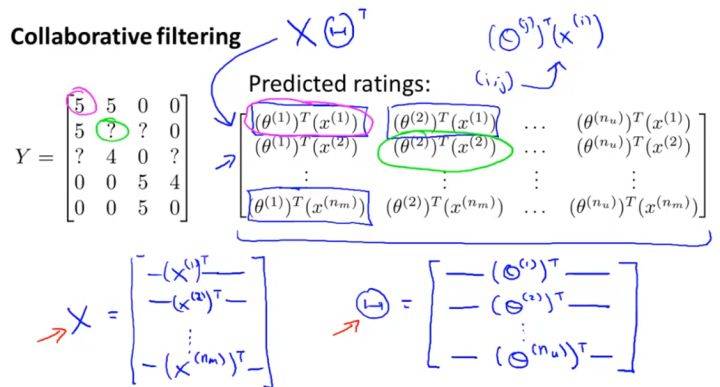
更为详细的表达如上图所示。矩阵 Y 可表示为 $\Theta^TX$ 。这个算法也叫低秩矩阵分解(Low Rank Matric Factorization)。
2. 均值标准化 Mean Normalization

当有一个用户什么电影都没有看过的话,我们用 $\Theta^TX$ 计算最后得到的结果全部都是一样的,并不能很好地推荐哪一部电影给他。

均值归一化要做的就是先计算每一行的平均值,再将每一个数据减去该行的平均值,得出一个新的评分矩阵。然后根据这个矩阵拟合出 $\Theta^TX$ ,最后的衡量结果加上平均值,即: $\Theta^TX+\mu_i$ 。而该 $\mu_i$ 就作为之前什么都没有的一个权值进行推荐。
四. Recommender Systems 测试
1. Question 1
Suppose you run a bookstore, and have ratings (1 to 5 stars) of books. Your collaborative filtering algorithm has learned a parameter vector θ(j) for user j, and a feature vector x(i) for each book. You would like to compute the "training error", meaning the average squared error of your system's predictions on all the ratings that you have gotten from your users. Which of these are correct ways of doing so (check all that apply)? For this problem, let m be the total number of ratings you have gotten from your users. (Another way of saying this is that $m=\sum^{n_m}_{i=1}\sum^{n_\mu}_{j=1}r(i,j))$. [Hint: Two of the four options below are correct.]
A.
B.
C.
D.
解答:A、B
2. Question 2
In which of the following situations will a collaborative filtering system be the most appropriate learning algorithm (compared to linear or logistic regression)?
A. You run an online bookstore and collect the ratings of many users. You want to use this to identify what books are "similar" to each other (i.e., if one user likes a certain book, what are other books that she might also like?)
B. You own a clothing store that sells many styles and brands of jeans. You have collected reviews of the different styles and brands from frequent shoppers, and you want to use these reviews to offer those shoppers discounts on the jeans you think they are most likely to purchase
C. You manage an online bookstore and you have the book ratings from many users. You want to learn to predict the expected sales volume (number of books sold) as a function of the average rating of a book.
D. You're an artist and hand-paint portraits for your clients. Each client gets a different portrait (of themselves) and gives you 1-5 star rating feedback, and each client purchases at most 1 portrait. You'd like to predict what rating your next customer will give you.
解答:A、B
协同过滤算法的要求是特征量和数据比较多。
A. 您运行在线书店并收集许多用户的评分。你想用这个来确定哪些书是彼此“相似”的(例如,如果一个用户喜欢某本书,她可能还喜欢其他书?)特征量很多,协同过滤。
B. 你拥有一家销售多种风格和品牌牛仔裤的服装店。您已经收集了来自经常购物者的不同款式和品牌的评论,并且您希望使用这些评论为您认为他们最有可能购买的牛仔裤提供这些购物者折扣。特征量很多,协同过滤。
C. 您可以管理在线书店,并拥有来自许多用户的图书评分。你想要学习预测预期销售量(出售书籍的数量)作为书籍平均评分的函数。用线性回归更好。
D. 你是一位艺术家,为你的客户提供手绘肖像画。每个客户都会获得不同的肖像(他们自己),并为您提供1-5星评级反馈,每位客户至多购买1张肖像。您想预测下一位客户给您的评分。用逻辑回归更好。
3. Question 3
You run a movie empire, and want to build a movie recommendation system based on collaborative filtering. There were three popular review websites (which we'll call A, B and C) which users to go to rate movies, and you have just acquired all three companies that run these websites. You'd like to merge the three companies' datasets together to build a single/unified system. On website A, users rank a movie as having 1 through 5 stars. On website B, users rank on a scale of 1 - 10, and decimal values (e.g., 7.5) are allowed. On website C, the ratings are from 1 to 100. You also have enough information to identify users/movies on one website with users/movies on a different website. Which of the following statements is true?
A. It is not possible to combine these websites' data. You must build three separate recommendation systems.
B. You can merge the three datasets into one, but you should first normalize each dataset separately by subtracting the mean and then dividing by (max - min) where the max and min (5-1) or (10-1) or (100-1) for the three websites respectively.
C. You can combine all three training sets into one as long as your perform mean normalization and feature scaling after you merge the data.
D. You can combine all three training sets into one without any modification and expect high performance from a recommendation system.
解答: B
做特征缩放。
4. Question 4
Which of the following are true of collaborative filtering systems? Check all that apply.
A. Even if each user has rated only a small fraction of all of your products (so r(i,j)=0 for the vast majority of (i,j) pairs), you can still build a recommender system by using collaborative filtering.
B. For collaborative filtering, it is possible to use one of the advanced optimization algoirthms (L-BFGS/conjugate gradient/etc.) to solve for both the $x^{(i)}$'s and $\theta^{(j)}$'s simultaneously.
C. For collaborative filtering, the optimization algorithm you should use is gradient descent. In particular, you cannot use more advanced optimization algorithms (L-BFGS/conjugate gradient/etc.) for collaborative filtering, since you have to solve for both the $x^{(i)}$'s and $\theta^{(j)}$'s simultaneously.
D. Suppose you are writing a recommender system to predict a user's book preferences. In order to build such a system, you need that user to rate all the other books in your training set.
解答:A、B
5. Question 5
Suppose you have two matrices A and B, where A is 5x3 and B is 3x5. Their product is C=AB, a 5x5 matrix. Furthermore, you have a 5x5 matrix R where every entry is 0 or 1. You want to find the sum of all elements C(i,j) for which the corresponding R(i,j) is 1, and ignore all elements C(i,j) where R(i,j)=0. One way to do so is the following code:

Which of the following pieces of Octave code will also correctly compute this total? Check all that apply. Assume all options are in code.
A. $total = sum(sum((A * B) .* R))$
B. $C = A * B; total = sum(sum(C(R == 1)))$;
C. $C = (A * B) * R; total = sum(C(:))$;
D. $total = sum(sum(A(R == 1) * B(R == 1))$;
解答:A、B
GitHub Repo:Halfrost-Field
Follow: halfrost · GitHub





