一. Gradient Descent with Large Datasets
如果我们有一个低方差的模型,增加数据集的规模可以帮助你获得更好的结果。我们应该怎样应对一个有100万条记录的训练集?
以线性回归模型为例,每一次梯度下降迭代,我们都需要计算训练集的误差的平方和,如果我们的学习算法需要有20次迭代,这便已经是非常大的计算代价。
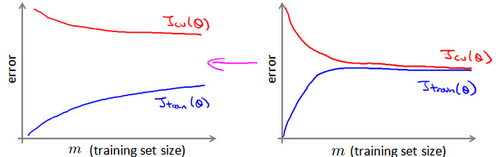
首先应该做的事是去检查一个这么大规模的训练集是否真的必要,也许我们只用1000个训练集也能获得较好的效果,我们可以绘制学习曲线来帮助判断。
二. Advanced Topics
1. 批量梯度下降法(Batch gradient descent)
拥有了大数据,就意味着,我们的算法模型中得面临一个很大的 m 值。回顾到我们的批量梯度下降法:
重复直到收敛:
$$\theta_j=\theta_j-\alpha \frac{1}{m} \sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}_j,\;\;\;\;for\;\;j=0,\cdots,n$$
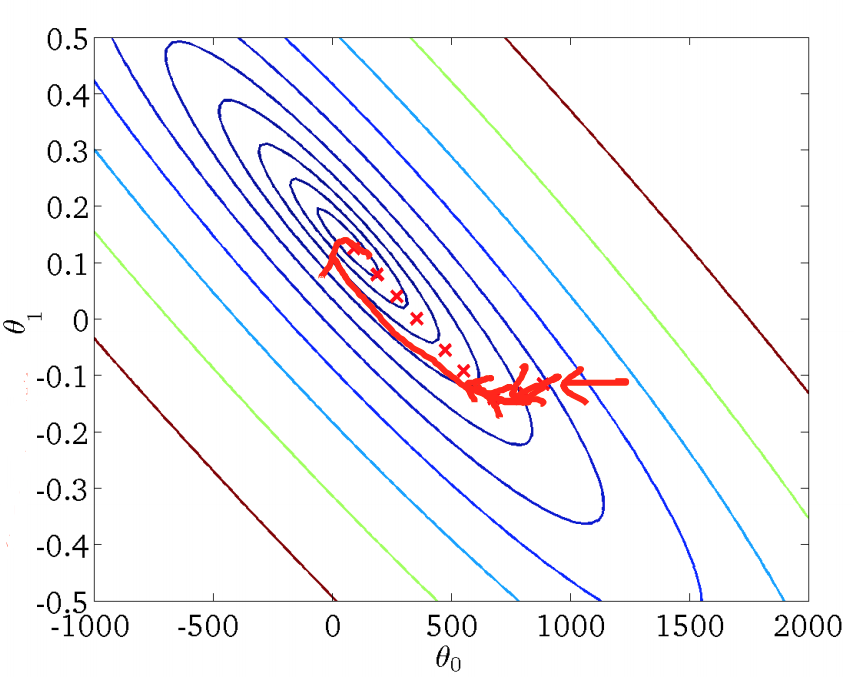
可以看到,每更新一个参数 $\theta_j$ ,我们都不得不遍历一遍样本集,在 m 很大时,该算法就显得比较低效。但是,批量梯度下降法能找到全局最优解:
2. 随机梯度下降法(Stochastic gradient descent)
针对大数据集,又引入了随机梯度下降法,该算法的执行过程为:
重复直到收敛:
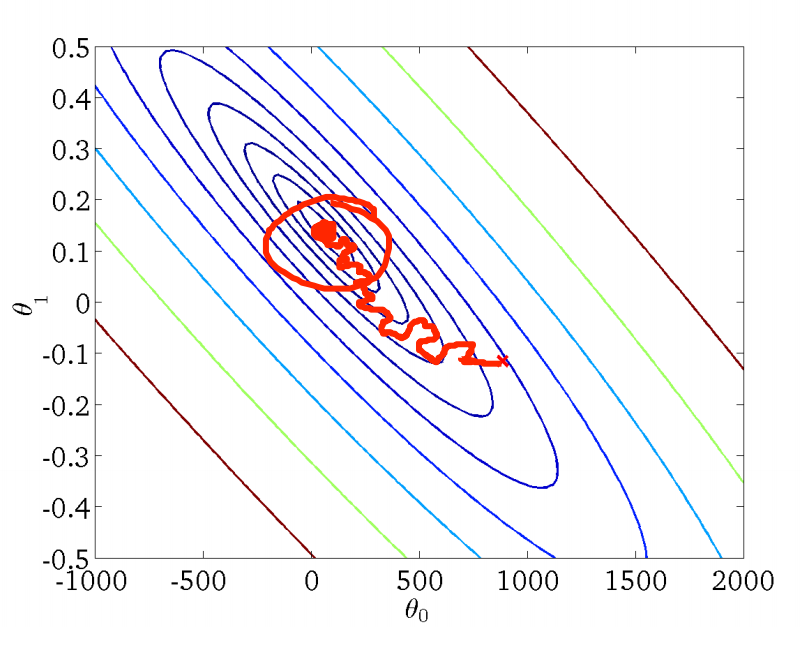
相较于批量梯度下降法,随机梯度下降法每次更新 $\theta_j$ 只会用当前遍历的样本。虽然外层循环仍需要遍历所有样本,但是,往往我们能在样本尚未遍历完时就已经收敛,因此,面临大数据集时,随机梯度下降法性能卓越。
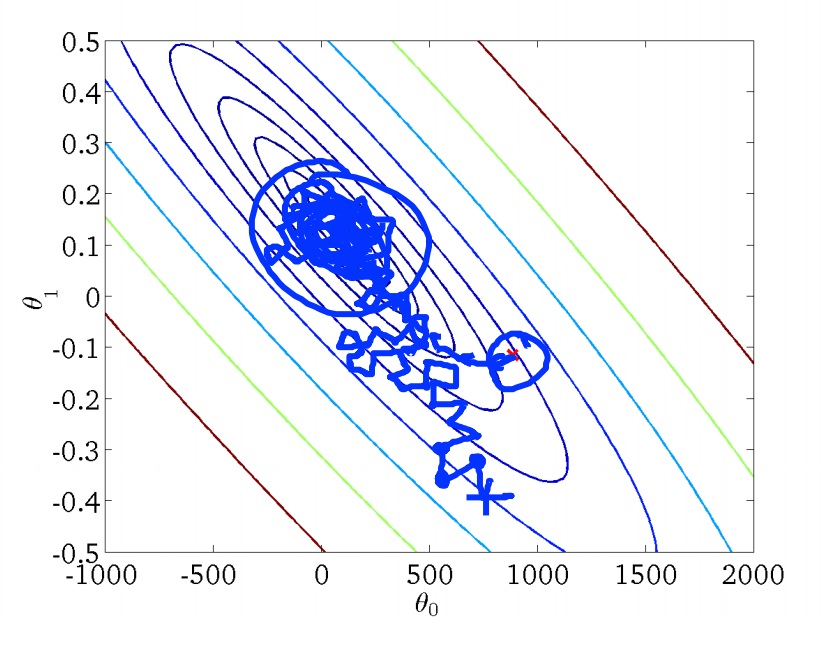
上图反映了随机梯度下降法找寻最优解的过程,相较于批量梯度下降法,随机梯度下降法的曲线就显得不是那么平滑,而是很曲折了,其也倾向于找到局部最优解而不是全局最优解。因此,我们通常需要绘制调试曲线来监控随机梯度的工作过程是否正确。例如,假定误差定义为 $cost(\theta,(x^{(i)},y^{(i)}))=\frac{1}{2}(h_\theta(x^{(i)})-y^{(i)})^2$,则每完成 1000 次迭代,即遍历了 1000 个样本,我们求取平均误差并进行绘制,得到误差随迭代次数的变化曲线:
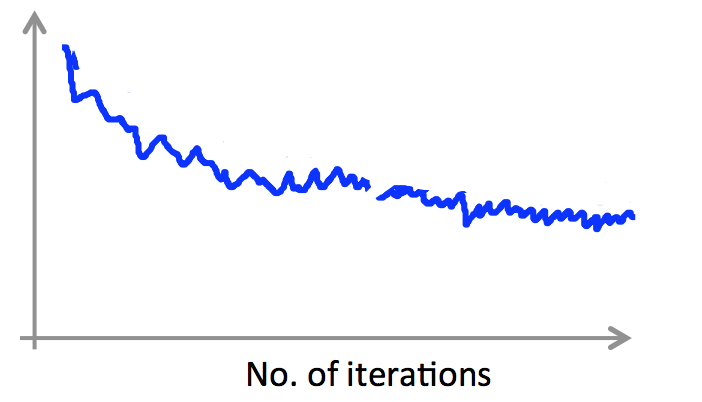
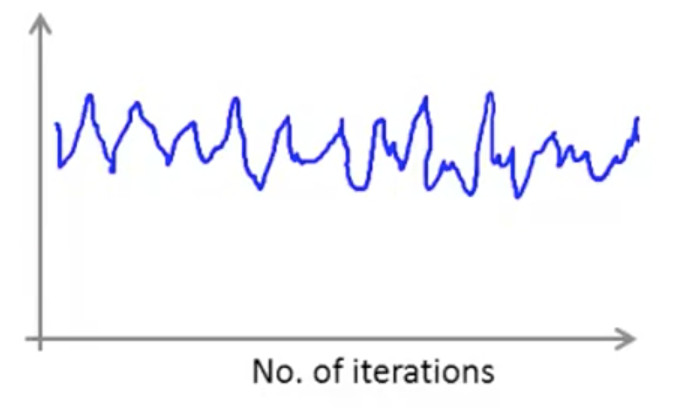
另外,遇到下面的曲线也不用担心,其并不意味着我们的学习率出了问题,有可能是我们的平均间隔取的太小:
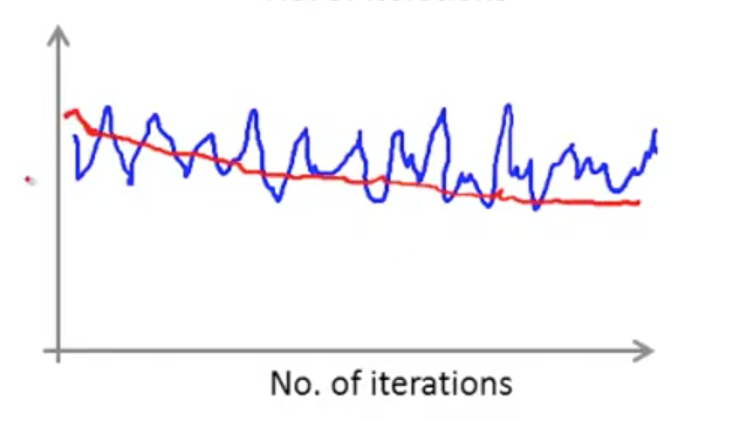
如果,我们每进行 5000 次迭代才进行绘制,那么曲线将更加平滑:
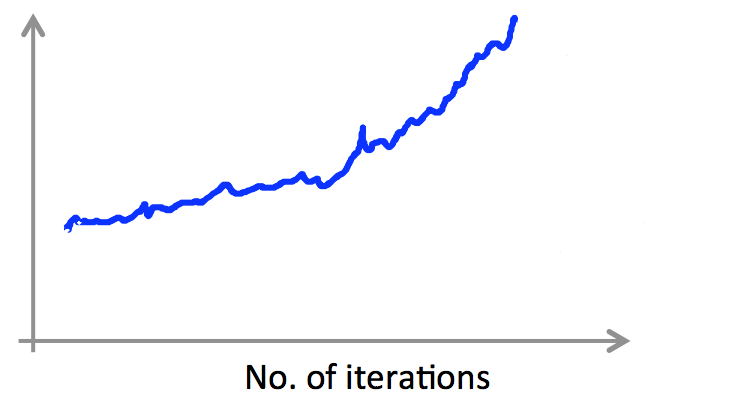
如果我们面临明显上升态势的曲线,就要考虑降低学习率 $\alpha$ 了:
学习率 $ \alpha $ 还可以随着迭代次数进行优化
$$\alpha=\frac{constant1}{iterationNumber+constant2}$$
随着迭代次数的增多,我们的下降步调就会放缓,避免出现抖动:
随机梯度下降法工作前,需要先随机化乱序数据集,是的遍历样本的过程更加分散。
3. Mini 批量梯度下降法(Mini-batch gradient descent)
Mini 批量梯度下降法是批量梯度下降法和随机梯度下降法的折中,通过参数 b 指明了每次迭代时,用于更新 $ \theta $ 的样本数。假定 b=10,m=1000 ,Mini 批量梯度下降法的工作过程如下:
重复直到收敛:
4. 在线学习
用户登录了某提供货运服务的网站,输入了货运的发件地址和收件地址,该网站给出了货运报价,用户决定是购买该服务( y=1 )或者是放弃购买该服务( y=0 )。
特征向量 x 包括了收发地址,报价信息,我们想要学习 $p(y=1|x;\theta)$ 来最优化报价:
重复直到收敛:
获得关于该用户的样本 (x,y),使用该样本更新 $\theta$:
这就是在线学习(Online learning),与前面章节提到的机器学习过程不同,在线学习并不需要一个固定的样本集进行学习,而是不断接收样本,不断通过接收到的样本进行学习。因此,在线学习的前提是:我们面临着流动的数据。
5. MapReduce
前面,我们提到了 Mini 批量梯度下降法,假定 b=400,m=400,000,000 ,我们对 $\theta$ 的优化就为:
$$\theta_j=\theta_j-\alpha \frac{1}{400} \sum i=1^{400}(h_\theta(x^i)-y^{(i)})x^{(i)}_j$$
假定我们有 4 个机器(Machine),我们首先通过 Map (映射) 过程来并行计算式中的求和项,每个机器被分配到 100 个样本进行计算:
最后,通过 Reduce(规约)操作进行求和:
$$\theta_j=\theta_j-\alpha \frac{1}{400}(temp_j^{(1)}+temp_j^{(2)}+temp_j^{(3)}+temp_j^{(4)})$$
我们可以使用多台机器进行 MapReduce,此时,Map 任务被分配到多个机器完成:

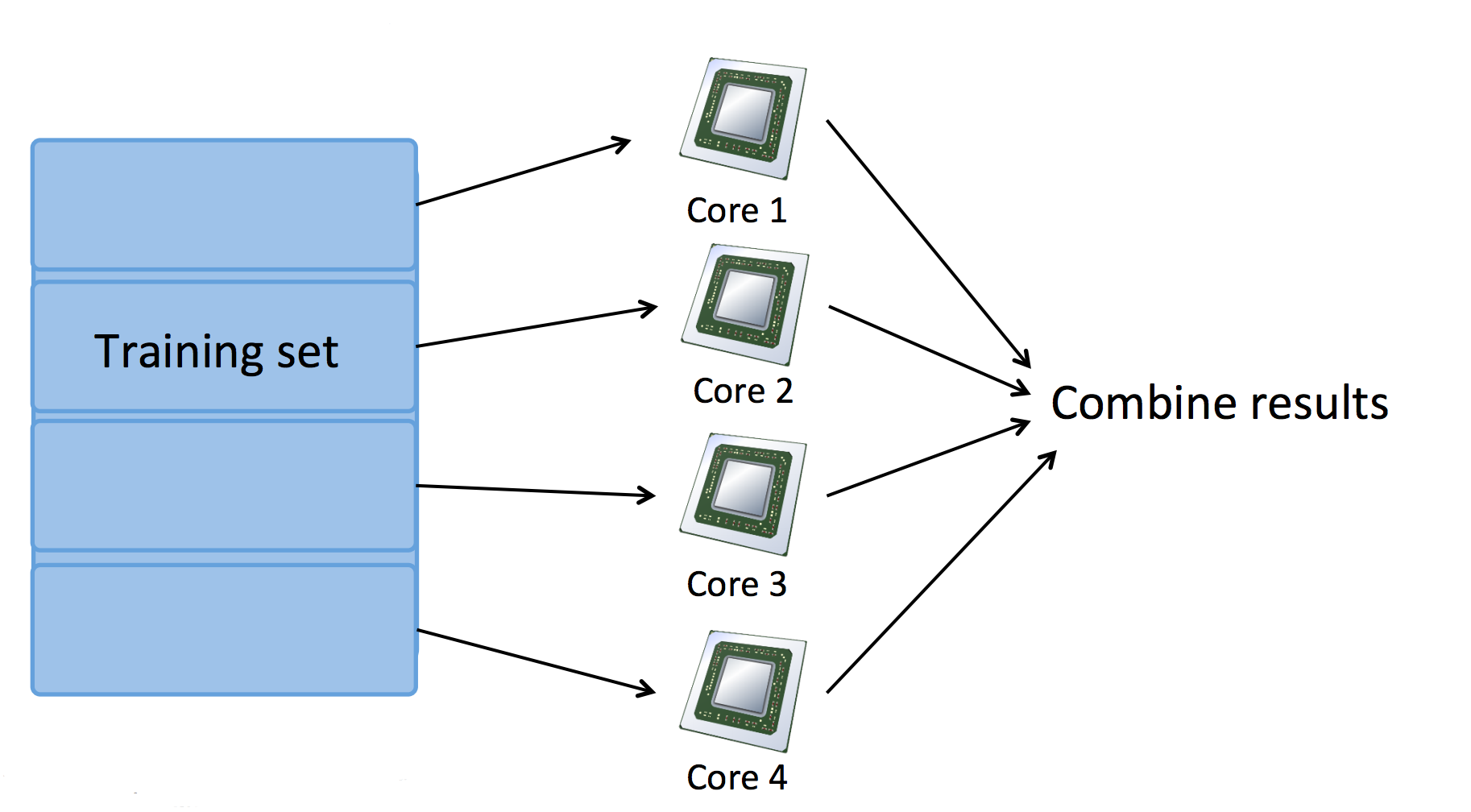
也可以使用单机多核心进行 MapReduce,此时,Map 任务被分配到多个 CPU 核心完成:
三. Large Scale Machine Learning 测试
1. Question 1
Suppose you are training a logistic regression classifier using stochastic gradient descent. You find that the cost (say, $cost(\theta,(x^{(i)},y^{(i)})$), averaged over the last 500 examples), plotted as a function of the number of iterations, is slowly increasing over time. Which of the following changes are likely to help?
A. Use fewer examples from your training set.
B. Try averaging the cost over a smaller number of examples (say 250 examples instead of 500) in the plot.
C. This is not possible with stochastic gradient descent, as it is guaranteed to converge to the optimal parameters $\theta$.
D. Try halving (decreasing) the learning rate $\alpha$, and see if that causes the cost to now consistently go down; and if not, keep halving it until it does.
解答:D
2. Question 2
Which of the following statements about stochastic gradient descent are true? Check all that apply.
A. Stochastic gradient descent is particularly well suited to problems with small training set sizes; in these problems, stochastic gradient descent is often preferred to batch gradient descent.
B. In each iteration of stochastic gradient descent, the algorithm needs to examine/use only one training example.
C. Suppose you are using stochastic gradient descent to train a linear regression classifier. The cost function $J(\theta)=\frac{1}{2m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2$ is guaranteed to decrease after every iteration of the stochastic gradient descent algorithm.
D. One of the advantages of stochastic gradient descent is that it can start progress in improving the parameters $\theta$ after looking at just a single training example; in contrast, batch gradient descent needs to take a pass over the entire training set before it starts to make progress in improving the parameters' values.
E. n order to make sure stochastic gradient descent is converging, we typically compute $J_{train}(\theta)$ after each iteration (and plot it) in order to make sure that the cost function is generally decreasing.
F. If you have a huge training set, then stochastic gradient descent may be much faster than batch gradient descent.
G. In order to make sure stochastic gradient descent is converging, we typically compute $J_{train}(\theta)$ after each iteration (and plot it) in order to make sure that the cost function is generally decreasing.
H. Before running stochastic gradient descent, you should randomly shuffle (reorder) the training set.
解答: F、H
C 错误
G 并不需要代价函数总是减少,可能会降低故错误
3. Question 3
Which of the following statements about online learning are true? Check all that apply.
A. Online learning algorithms are most appropriate when we have a fixed training set of size m that we want to train on.
B. Online learning algorithms are usually best suited to problems were we have a continuous/non-stop stream of data that we want to learn from.
C. When using online learning, you must save every new training example you get, as you will need to reuse past examples to re-train the model even after you get new training examples in the future.
D. One of the advantages of online learning is that if the function we're modeling changes over time (such as if we are modeling the probability of users clicking on different URLs, and user tastes/preferences are changing over time), the online learning algorithm will automatically adapt to these changes.
解答: B、D
4. Question 4
Assuming that you have a very large training set, which of the following algorithms do you think can be parallelized using map-reduce and splitting the training set across different machines? Check all that apply.
A. Logistic regression trained using batch gradient descent.
B. Linear regression trained using stochastic gradient descent.
C. Logistic regression trained using stochastic gradient descent.
D. Computing the average of all the features in your training set $\mu=\frac{1}{m}\sum^m_{i=1}x^{(i)}$ (say in order to perform mean normalization).
解答: A、D
可以用映射约减算法的有用批量梯度下降的逻辑回归,凡是要计算大量值的算法,用随机梯度下降不用计算大量的值故选 A、D
B. Linear regression trained using batch gradient descent. 所以 B 错误
C. 错误
5. Question 5
Which of the following statements about map-reduce are true? Check all that apply.
A. When using map-reduce with gradient descent, we usually use a single machine that accumulates the gradients from each of the map-reduce machines, in order to compute the parameter update for that iteration.
B. Linear regression and logistic regression can be parallelized using map-reduce, but not neural network training.
C. Because of network latency and other overhead associated with map-reduce, if we run map-reduce using N computers, we might get less than an N-fold speedup compared to using 1 computer.
D. If you have only 1 computer with 1 computing core, then map-reduce is unlikely to help.
E. If you have just 1 computer, but your computer has multiple CPUs or multiple cores, then map-reduce might be a viable way to parallelize your learning algorithm.
F. In order to parallelize a learning algorithm using map-reduce, the first step is to figure out how to express the main work done by the algorithm as computing sums of functions of training examples.
G. Running map-reduce over N computers requires that we split the training set into $N^2$ pieces.
解答:A、C、D
用N台电脑比用一台,要快不到 N 倍。用一台计算机统计其他计算出来的数据。神经网络也要计算代价函数也要有大量计算,所以神经网络也可以并行计算。
B 错误
C 正确
E 错误
F 错误
G 可能正确?
GitHub Repo:Halfrost-Field
Follow: halfrost · GitHub





