初探神经网络

一. Motivations

假如我们用之前的逻辑回归解决以下分类问题：

我们需要构造一个有很多项的非线性的逻辑回归函数。当只有两个特征量的时候，这还算比较简单的，但是假如我们有100个特征量呢？我们只考虑二阶项的话，其二阶项的个数大约是 $\frac{n^2}{2}$ 。假如我们要包含所有的二阶项的话这样看起来不是一个好办法，因为项数实在太多运算量也很多，而且最后结果往往容易造成过拟合。当然我们只是考虑了二阶项，考虑二阶项以上的就更多了。

当初始特征个数 n 增大时，这些高阶多项式项数将以几何级数上升，特征空间也会随之急剧膨胀。所以当特征个数 n比较大的时候，用这个方法建立分类器并不是一个好的做法。

而对于大多数的机器学习问题， n 一般是比较大的。

对一个拥有很多特征的复杂数据集进行线性回归是代价很高的。比如我们对 50 * 50 像素的黑白图分类，我们就拥有了 2500 个特征。如果我们还要包含所有二次特征，复杂度为 $O(n^{2}/2)$，也就是说一共要有 $2500^{2}/2=3125000$ 个特征。这样计算的代价是高昂的。

人工神经网络是对具有很多特征的复杂问题进行机器学习的一种方法。

二. Neural Networks

人工神经网络是对生物神经网络的一种简化的模拟。那么，我们先从生物中的神经元入手，进而了解神经网络的工作方式。

用一个简单的模型来模拟神经元的工作，我们将神经元模拟成一个逻辑单元：

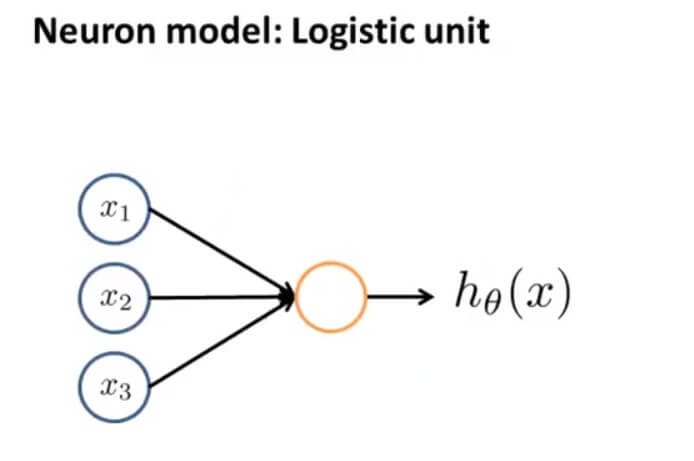
$x_{1},x_{2},x_{3}$ 可以将其看成输入神经树突，黄色的圆圈则可以看成中心处理器细胞核， $h_\theta(x)$ 则可看成输出神经轴突。因为这里是逻辑单元，所以我们的输出函数为： $h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}}$ 。一般我们把这称为一个有 s 型函数（逻辑函数）作为激励的人工神经元。

那么神经网络其实就是这些神经元组合在一起的集合，如下图：

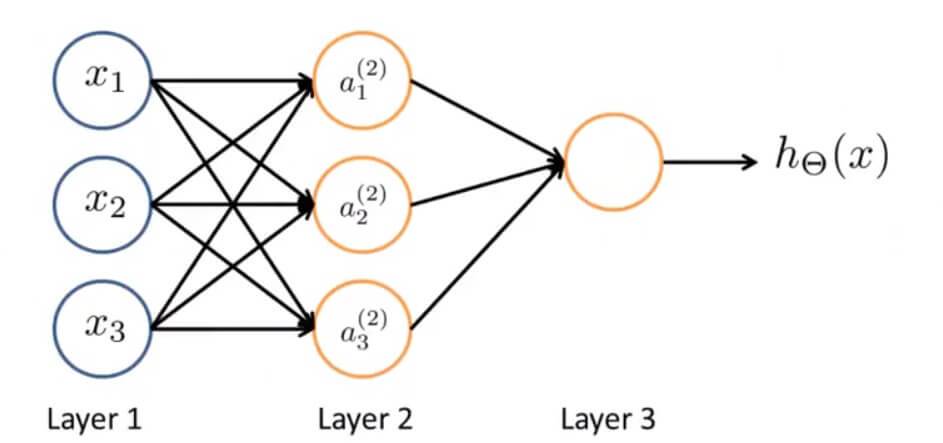
左边第一层 Layer1 被称为输入层。在输入层我们输入我们的特征项 $x_{1},x_{2},x_{3}$ 。

右边最后一层被称为输出层。输出函数为： $h_\Theta(x)$ 。

中间这层被称为隐藏层。

我们现在要计算当前神经元的值，在当前神经元所在层的前一层，有很多个突触前神经元（当前神经元也是相对于他们的突触后神经元）。

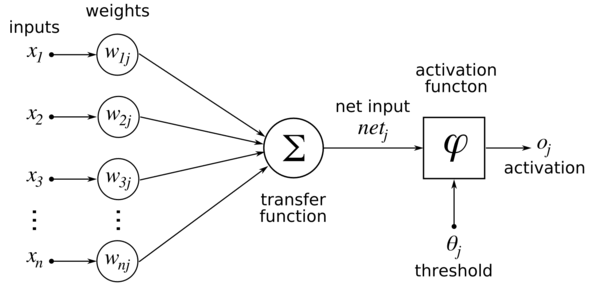
对于前一层的每一个突触前神经元，都有一个输出值，作为当前神经元的输入值，经过轴突传递到当前神经元。当然，如果是第一层神经元，则直接从输入样本数据中接受刺激（对应图中的 $x_{i}$）。

轴突具有权值（对应图中的权值 weights 列：$w_{ij}$），对每一个输出值加权求和，得到该神经元的输入值。这个加权求和对应图中的transfer function（转移函数），但这个函数的名称并不明确，有人把它称作激活函数（activation function），不同的人可能有不同的叫法，这里仅供参考。

得到了该神经元的值，就要判定该神经元是否激活兴奋。这对应于图中的activation function（激活函数），但也有人将这个函数叫做输出函数（output function），而把前面说的那一部分叫做激活函数（activation function），并把这两部分合称为转移函数（transfer function）。

有几种函数可以作为激活函数：

阶跃函数。这是最简单直接的形式，也是人工神经网络定义时一般采用的。
逻辑函数。就是S型函数（Sigmoid函数），具有可无限微分的优势。
斜坡函数
高斯函数
…

可以注意到图中的threshold（阈值），$\theta_{j}$，即激活阈值。也就是说，仅当神经元的值大于这个阈值时，该神经元激活兴奋，输出1；否则无法激活，输出0。

其中隐藏层中的元素我们用 $a_i^{(j)}$ 表示。上标 j 表示的是第几层（有时候我们并不只有简单一层），下标 i 表示第几个，第j层的第i个节点（神经元）的“激活值”。

上面的神经网络可以简单的表示为：

$$\begin{bmatrix} x_{0}\\ x_{1}\\ x_{2}\\ x_{3} \end{bmatrix} \rightarrow \begin{bmatrix} a_{1}^{(2)}\\ a_{2}^{(2)}\\ a_{3}^{(2)} \end{bmatrix} \rightarrow h_{\theta}(x) $$

左边输入层多增加了一个偏置单元(偏置神经元)，$x_{0}$

用 $\Theta^{(j)}$ 表示特征量前的参数，是一个有权重的矩阵控制着一层参数的大小，映射第j层到第j+1层的权值矩阵。

上述的神经网络可用数学表达，如下：

$$ \begin{align*} a_{1}^{(2)} &= g(\Theta_{10}^{(1)}x_{0}+\Theta_{11}^{(1)}x_{1}+\Theta_{12}^{(1)}x_{2}+\Theta_{13}^{(1)}x_{3}) \\ a_{2}^{(2)} &= g(\Theta_{20}^{(1)}x_{0}+\Theta_{21}^{(1)}x_{1}+\Theta_{22}^{(1)}x_{2}+\Theta_{23}^{(1)}x_{3}) \\ a_{3}^{(2)} &= g(\Theta_{30}^{(1)}x_{0}+\Theta_{31}^{(1)}x_{1}+\Theta_{32}^{(1)}x_{2}+\Theta_{33}^{(1)}x_{3}) \\ h_{\Theta}(x) &= a_{1}^{(3)} = g(\Theta_{10}^{(2)}a_{0}^{(2)}+\Theta_{11}^{(2)}a_{1}^{(2)}+\Theta_{12}^{(2)}a_{2}^{(2)}+\Theta_{13}^{(2)}a_{3}^{(2)}) \\ \end{align*} $$

$\Theta$ 矩阵也被称作为模型的权重。这里的 $g(x)$ 都是 sigmoid 激活函数，即 $g(x) = \frac{1}{1+e^{-x}}$

对上面的神经网络数学表达方式进行向量化推导，令：

$$ \begin{align*} z_{1}^{(2)} &= \Theta_{10}^{(1)}x_{0}+\Theta_{11}^{(1)}x_{1}+\Theta_{12}^{(1)}x_{2}+\Theta_{13}^{(1)}x_{3} \\ z_{2}^{(2)} &= \Theta_{20}^{(1)}x_{0}+\Theta_{21}^{(1)}x_{1}+\Theta_{22}^{(1)}x_{2}+\Theta_{23}^{(1)}x_{3} \\ z_{3}^{(2)} &= \Theta_{30}^{(1)}x_{0}+\Theta_{31}^{(1)}x_{1}+\Theta_{32}^{(1)}x_{2}+\Theta_{33}^{(1)}x_{3} \\ \vdots \\ z_{k}^{(2)} &= \Theta_{k,0}^{(1)}x_{0}+\Theta_{k,1}^{(1)}x_{1}+\Theta_{k,2}^{(1)}x_{2}+\Theta_{k,3}^{(1)}x_{3} \\ \end{align*} $$

于是可以得到：

$$ \begin{align*} a_{1}^{(2)} &= g(z_{1}^{(2)}) \\ a_{2}^{(2)} &= g(z_{2}^{(2)}) \\ a_{3}^{(2)} &= g(z_{3}^{(2)}) \\ \end{align*} $$

用向量即可表示为：

$$x = \begin{bmatrix} x_{0}\\ x_{1}\\ x_{2}\\ x_{3} \end{bmatrix},z^{(2)} = \begin{bmatrix} z_{1}^{(2)}\\ z_{2}^{(2)}\\ z_{3}^{(2)}\\ \end{bmatrix} = \Theta^{(1)}x$$

统一一下前后两层的输入输出关系，将 $x=a^{(1)}$，即可得到：

$$ \begin{align*} x &= \begin{bmatrix} x_{0}\\ x_{1}\\ \vdots \\ x_{n} \end{bmatrix},z^{(j)} = \begin{bmatrix} z_{1}^{(j)}\\ z_{2}^{(j)}\\ \vdots \\ z_{3}^{(j)}\\ \end{bmatrix}, \\ \Rightarrow z^{(j)} &=\Theta^{(j-1)}a^{(j-1)}\\ \end{align*} $$

这里也可以得到一个结论：

假如一个网络里面在第 j 层有 $s_j$ 个单元，在第 j+1 层有 $s_{j+1}$ 个单元，那么 $\Theta^{(j)}$ 则控制着第 j 层到第 j+1 层的映射矩阵，矩阵的维度是： $s_{j+1} * (s_j + 1)$ 。(例如： j=1 , $s_j=1$， $s_{j+1}$=1 ，也就是说第一层只有一个单元，第二层也只有一个单元，那么 $\Theta^{(1)}$ 矩阵维度就是 1 * 2 ,因为要算上偏置单元)

因为我们通常有 $a_0^{(j)}=1$ ，所以：

$$ \begin{align*} a^{(j)}&=g(z^{(j)})\\ z^{(j+1)}&=\Theta^{(j)}a^{(j)}\\ h_\Theta(x)&=a^{(j+1)}=g(z^{(j+1)})\\ \end{align*} $$

由这个关系其实可以看出，神经网络跟之前所学的逻辑回归根本区别在于，它是将上一层的输出当做下一层的输入，这个从输入层到隐藏层再到输出层一次计算激励的过程叫做 forward propagation（前向传播）。

三. Applications

1. 逻辑运算

利用神经网络进行逻辑与运算

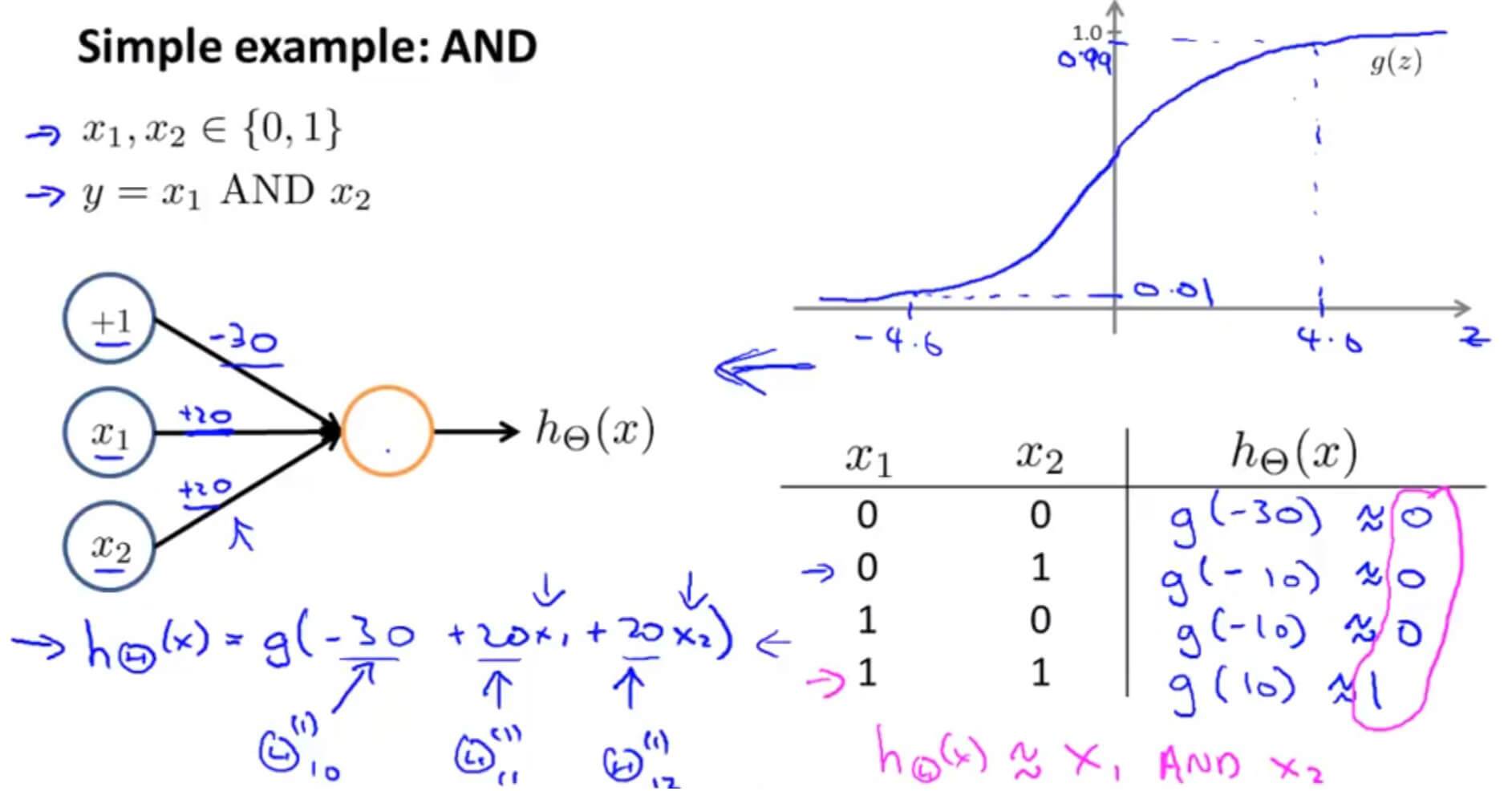
利用神经网络进行逻辑非运算

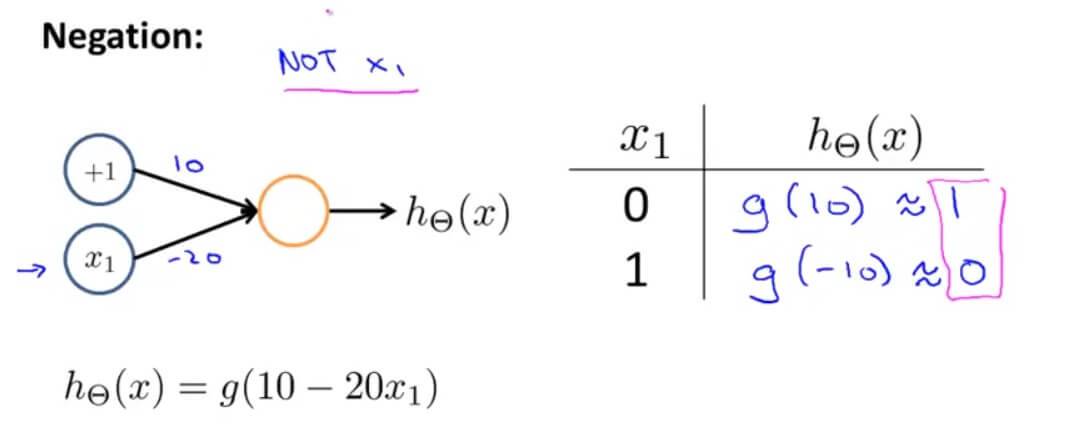
但是单一一层无法完成异或运算。

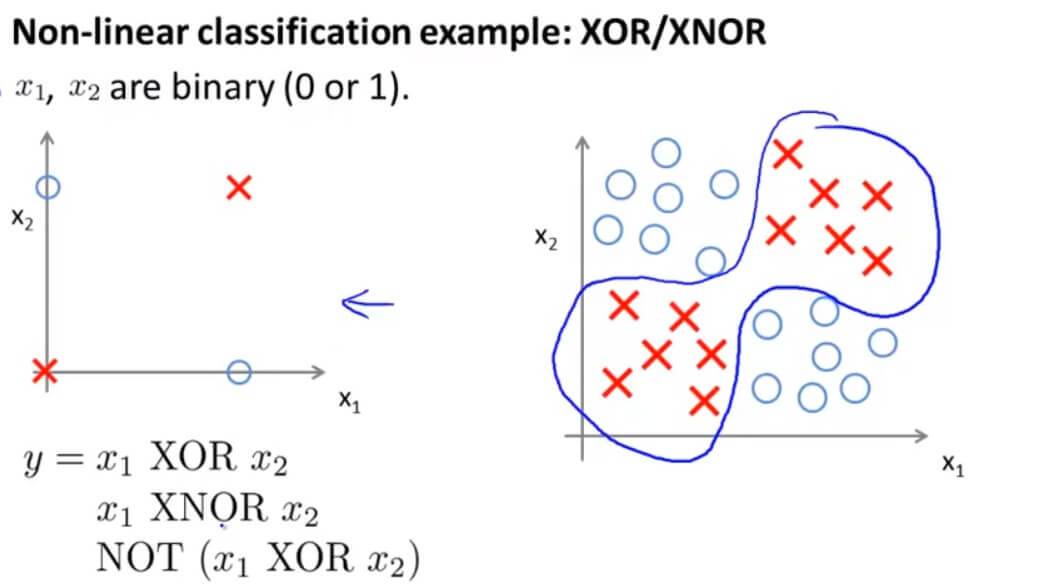
异或在几何上的问题其实是将红叉和蓝圈分开，但是我们的输出函数是： $h_\Theta(x)=g(\Theta_{10}^{(1)}x_0+\Theta_{11}^{(1)}x_1+\Theta_{12}^{(1)}x_2)$ ,这是线性的，那么在图上无论怎么画一条直线，也没有办法将两个不同的训练集分开。既然一条直线不行，那么神经网络增加一层。

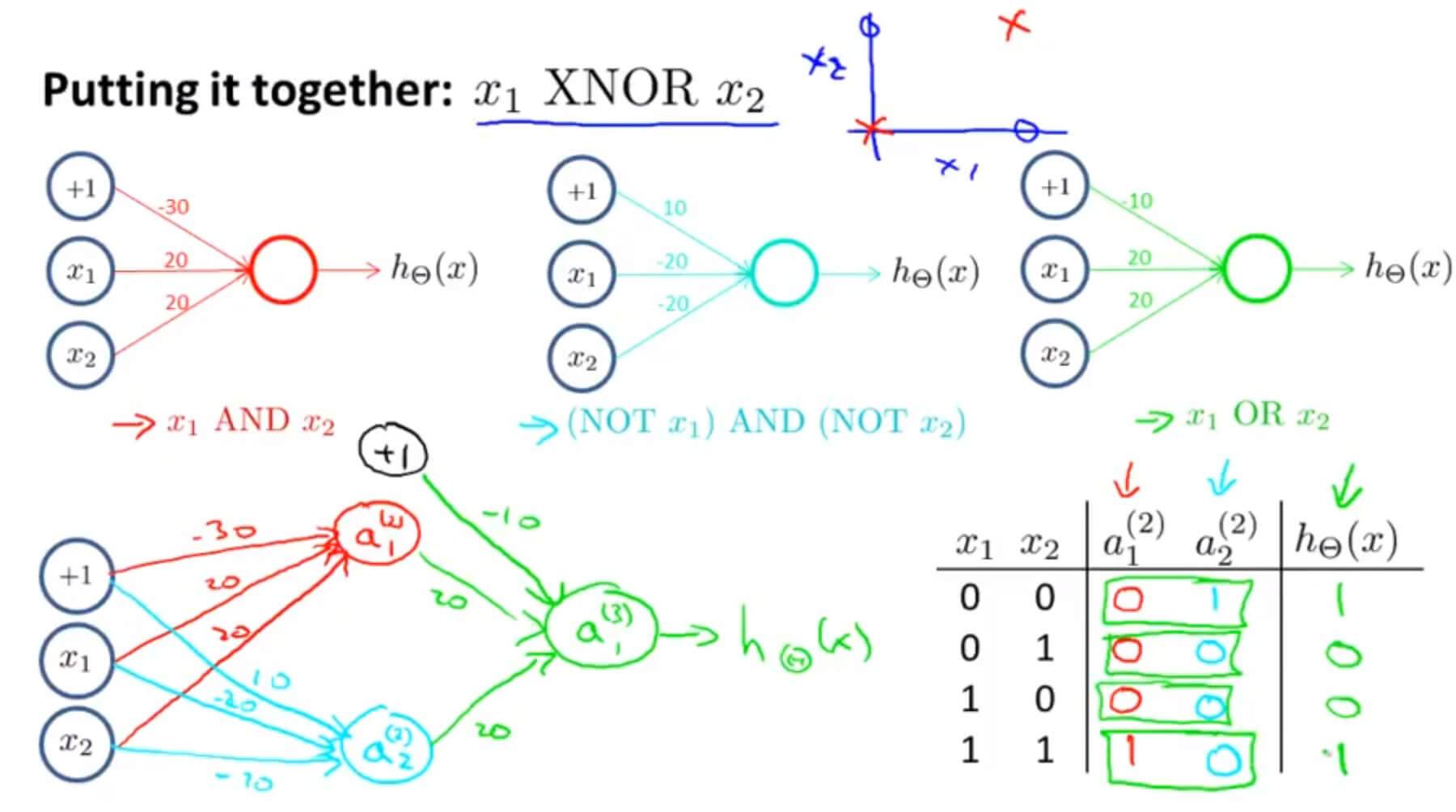
如上图，将第二层第一个元素 $a_1^{(2)}$ 作为与运算的结果，第二个元素 $a_2^{(2)}$ 作为或非运算的结果， $a_1^{(2)}$ 和 $a_2^{(2)}$ 再作为输入，进行或运算，作为第三层输出的结果，最后得到的结果与输入的关系正是异或运算的关系。

2. 本质

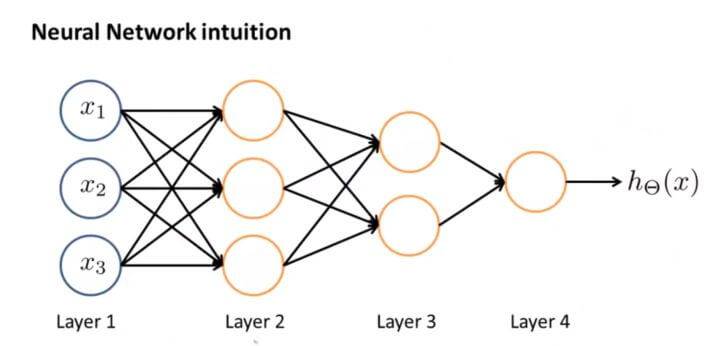
神经网络正是这样解决比较复杂的函数，当层数很多的时候，我们有一个相对简单的输入量，通过加以权重和不同的运算送到第二层，而第三层在第二层作为输入的基础上再来进行一些更复杂的运算，一层一层下去解决问题。

四. Neural Networks: Representation 测试

1. Question 1

Which of the following statements are true? Check all that apply.

A. Suppose you have a multi-class classification problem with three classes, trained with a 3 layer network. Let a(3)1=(hΘ(x))1 be the activation of the first output unit, and similarly a(3)2=(hΘ(x))2 and a(3)3=(hΘ(x))3. Then for any input x, it must be the case that a(3)1+a(3)2+a(3)3=1.

B. The activation values of the hidden units in a neural network, with the sigmoid activation function applied at every layer, are always in the range (0, 1).

C. A two layer (one input layer, one output layer; no hidden layer) neural network can represent the XOR function.

D. Any logical function over binary-valued (0 or 1) inputs x1 and x2 can be (approximately) represented using some neural network.

解答： B、D

B.S型函数作为判断函数运用到每一层，其范围是[0,1]，正确。
D.任何二进制输入的逻辑运算都可以神经网络解决，正确。
C.异或不可以用一层神经网络解决。
A.不一定，决策函数不是S型函数的话最后结果相加就不是1了。

GitHub Repo：Halfrost-Field

Follow: halfrost · GitHub

Source: https://github.com/halfrost/Halfrost-Field/blob/master/contents/Machine_Learning/Neural_Networks_Representation.ipynb

Tags

初探神经网络

一. Motivations

二. Neural Networks