一. Classification and Representation
要尝试分类,一种方法是使用线性回归,并将所有大于0.5的预测值映射为1,将小于0.5的所有预测值映射为0.但是,此方法效果不佳,因为分类实际上不是线性函数。 分类问题就像回归问题一样,除了我们现在想要预测的值只有少数离散值。
线性回归用来解决分类问题,通常不是一个好主意。
我们解决分类问题,忽略y是离散值,并使用我们的旧线性回归算法来尝试预测给定的x。但是,构建这种方法性能很差的示例很容易。直观地说,当知道$y\in \begin{Bmatrix}
0,1
\end{Bmatrix}$时,$h_{\theta}(x)$ 取大于1或小于0的值也是没有意义的。为了解决这个问题,让我们改变我们的假设 $h_{\theta}(x)$ 的形式以满足 $0\leqslant h_{\theta}(x)\leqslant 1$。这是通过将 $\theta^{T}x$ 插入 Logistic 函数来完成的:
$$g(x) = \frac{1}{1+e^{-x}}$$
上式称为 Sigmoid Function 或者 Logistic Function
令 $h_{\theta}(x) = g(\theta^{T}x)$,$z = \theta^{T}x$,则:
$$g(x) = \frac{1}{1+e^{-\theta^{T}x}}$$
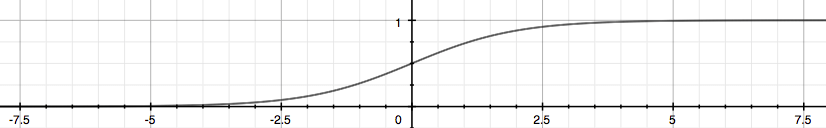
这里显示的函数$g(x)$将任何实数映射到(0,1)区间,使得它可用于将任意值函数转换为更适合分类的函数。
决策边界不是训练集的属性,而是假设本身及其参数的属性。
二. Logistic Regression Model
1. Cost Function
之前定义的代价函数:
$$ \rm{CostFunction} = \rm{F}({\theta}) = \frac{1}{m}\sum_{i = 1}^{m} (h_{\theta}(x^{(i)})-y^{(i)})^2 $$
如果将 $$h_{\theta}(x) = \frac{1}{1+e^{-\theta^{T}x}} $$ 代入到上面的式子中,$\rm{CostFunction}$ 的函数图像会是一个非凸函数,会有很多个局部极值点。
于是我们重新寻找一个新的代价函数:
需要说明的一点是,在我们的训练集中,甚至不在训练集中的样本,y 的值总是等于 0 或者 1 。
2. Simplified Cost Function and Gradient Descent
于是进一步我们把代价函数写成一个式子:
$$\rm{Cost}(h_{\theta}(x),y) = - ylog(h_{\theta}(x)) - (1-y)log(1-h_{\theta}(x))$$
所以代价函数最终表示为:
向量化形式:
为了把式子写成上面这样子是来自于统计学的极大似然估计法得来的,它是统计学里为不同的模型快速寻找参数的方法。它的性质之一是它是凸函数。
利用梯度下降的方法,得到代价函数的最小值:
$$ \theta_{j} := \theta_{j} - \alpha \frac{1}{m} \sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}_{j}$$
矢量化,即:
$$ \theta := \theta - \alpha \frac{1}{m} X^{T}(g(X\Theta)-\vec{y})$$
这里需要注意的是,
线性回归中,$h_{\theta}(x) = \theta^{T}x $,
而 Logistic 回归中,$h_{\theta}(x) = \frac{1}{1+e^{-\theta^{T}x}}$ 。
最后,特征缩放的方法同样适用于 Logistic 回归,让其梯度下降收敛更快。
3. 求导过程
逻辑函数
我们先来看看如何对逻辑函数(Sigmoid函数)求导:
代价函数
利用上面的结果,借助复合函数求导公式等,可得:
向量化形式:
4. Advanced Optimization
除去梯度下降法,还有其他的优化方法,
conjugate gradient 共轭梯度法,
BFGS,
L_BFGS,
上述3种算法在高等数值计算中。它们相比梯度下降,有以下一些优点:
- 不需要手动选择学习率 $\alpha$ 。可以理解为它们有一个智能的内循环(线搜索算法),它会自动尝试不同的学习速率 $\alpha$,并自动选择一个最好的学习速率 $\alpha$ 。甚至还可以为每次迭代选择不同的学习速率,那么就不需要自己选择了。
- 收敛速度远远快于梯度下降。
缺点就是相比梯度下降而言,更加复杂。
举个例子:
function [jVal, gradient] = costFunction(theta)
jVal = (theta(1)-5)^2 + (theta(2)-5)^2;
gradient = zeros(2,1);
gradient(1) = 2*(theta(1)-5);
gradient(2) = 2*(theta(2)-5);
调用高级函数 fminunc:
options = optimset('GrabObj','on','MaxIter','100');
initialTheta = zeros(2,1);
[optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);
最终结果:
optTheta =
5.0000
5.0000
functionVal = 1.5777e-030
exitFlag = 1
optTheta 表示的是最终求得的结果,functionVal 表示的是代价函数的最小值,这里是 0,是我们期望的。exitFlag 表示的是最终是否收敛,1表示收敛。
这里的 fminunc 是试图找到一个多变量函数的最小值,从一个估计的初试值开始,这通常被认为是无约束非线性优化问题。
另外一些例子:
x =fminunc(fun,x0) %试图从x0附近开始找到函数的局部最小值,x0可以是标量,向量或矩阵
x =fminunc(fun,x0,options) %根据结构体options中的设置来找到最小值,可用optimset来设置options
x =fminunc(problem) %为problem找到最小值,而problem是在Input Arguments中定义的结构体
[x,fval]= fminunc(...) %返回目标函数fun在解x处的函数值
[x,fval,exitflag]= fminunc(...) %返回一个描述退出条件的值exitflag
[x,fval,exitflag,output]= fminunc(...) %返回一个叫output的结构体,它包含着优化的信息
[x,fval,exitflag,output,grad]= fminunc(...) %返回函数在解x处的梯度的值,存储在grad中
[x,fval,exitflag,output,grad,hessian]= fminunc(...) %返回函数在解x处的Hessian矩阵的值,存储在hessian中
三. Multiclass Classification
这一章节我们来讨论一下如何利用逻辑回归来解决多类别分类问题。介绍一个一对多的分类算法。

现在,当我们有两个以上的类别时,我们将处理数据的分类。我们将扩展我们的定义,使得y = {0,1 ... n},而不是y = {0,1}。 由于y = {0,1 ... n},我们将问题分成n + 1(+1,因为索引从0开始)二元分类问题;在每一个中,我们都预测'y'是我们其中一个类的成员的概率。
最终在 n + 1 个分类器中分别输入 x ,然后取这 n + 1 个分类器概率的最大值,即是对应 $y=i$ 的概率值。
四. Logistic Regression 测试
1. Question 1
Suppose that you have trained a logistic regression classifier, and it outputs on a new example x a prediction hθ(x) = 0.7. This means (check all that apply):
A. Our estimate for P(y=1|x;θ) is 0.7.
B. Our estimate for P(y=0|x;θ) is 0.3.
C. Our estimate for P(y=1|x;θ) is 0.3.
D. Our estimate for P(y=0|x;θ) is 0.7.
解答: A、B
2. Question 2
Suppose you have the following training set, and fit a logistic regression classifier hθ(x)=g(θ0+θ1x1+θ2x2).
Which of the following are true? Check all that apply.
A. Adding polynomial features (e.g., instead using hθ(x)=g(θ0+θ1x1+θ2x2+θ3x21+θ4x1x2+θ5x22) ) could increase how well we can fit the training data.
B. At the optimal value of θ (e.g., found by fminunc), we will have J(θ)≥0.
C. Adding polynomial features (e.g., instead using hθ(x)=g(θ0+θ1x1+θ2x2+θ3x21+θ4x1x2+θ5x22) ) would increase J(θ) because we are now summing over more terms.
D. If we train gradient descent for enough iterations, for some examples x(i) in the training set it is possible to obtain hθ(x(i))>1.
解答: A、B
3. Question 3
For logistic regression, the gradient is given by ∂∂θjJ(θ)=1m∑mi=1(hθ(x(i))−y(i))x(i)j. Which of these is a correct gradient descent update for logistic regression with a learning rate of α? Check all that apply.
A. θj:=θj−α1m∑mi=1(hθ(x(i))−y(i))x(i) (simultaneously update for all j).
B. θj:=θj−α1m∑mi=1(hθ(x(i))−y(i))x(i)j (simultaneously update for all j).
C. θj:=θj−α1m∑mi=1(11+e−θTx(i)−y(i))x(i)j (simultaneously update for all j).
D. θ:=θ−α1m∑mi=1(θTx−y(i))x(i).
解答: A、D
线性回归与逻辑回归的区别
4. Question 4
Which of the following statements are true? Check all that apply.
A. The cost function J(θ) for logistic regression trained with m≥1 examples is always greater than or equal to zero.
B. Linear regression always works well for classification if you classify by using a threshold on the prediction made by linear regression.
C. The one-vs-all technique allows you to use logistic regression for problems in which each y(i) comes from a fixed, discrete set of values.
D. For logistic regression, sometimes gradient descent will converge to a local minimum (and fail to find the global minimum). This is the reason we prefer more advanced optimization algorithms such as fminunc (conjugate gradient/BFGS/L-BFGS/etc).
解答: A、C
D由于使用代价函数为线性回归代价函数,会有很多局部最优值
5. Question 5
Suppose you train a logistic classifier hθ(x)=g(θ0+θ1x1+θ2x2). Suppose θ0=6,θ1=0,θ2=−1. Which of the following figures represents the decision boundary found by your classifier?
解答: C
6-x2>=0 即X2<6时为1
GitHub Repo:Halfrost-Field
Follow: halfrost · GitHub





