笔者在《高效的多维空间点索引算法 — Geohash 和 Google S2》文章中详细的分析了 Google S2 的算法实现思想。文章发出来以后,一部分读者对它的实现产生了好奇。本文算是对上篇文章的补充,将从代码实现的角度来看看 Google S2 的算法具体实现。建议先读完上篇文章里面的算法思想,再看本篇的代码实现会更好理解一些。
一. 什么是 Cell ?
Google S2 中定义了一个将单位球体分解成单元格层次结构的框架。每个 Cell 的单元格是由四个测地线限定的四边形。通过将立方体的六个面投影到单位球上来获得层级的顶层,通过递归地将每个单元细分为四个子层来获得较低层。例如,下面的图片显示了六个 face 中 Cell 的两个,其中一个已经细分了几次:
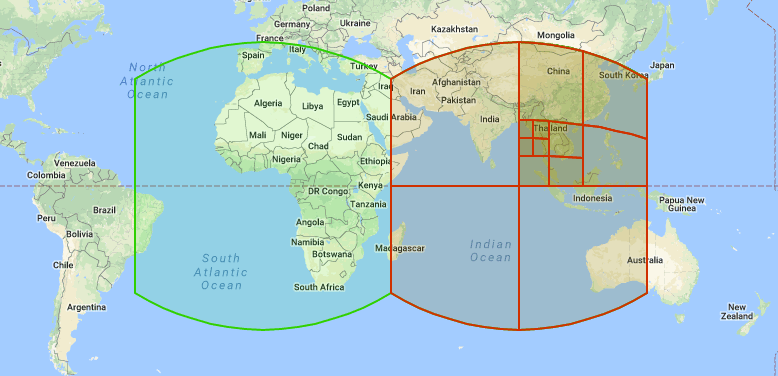
注意 Cell 边缘似乎是弯曲的,这是因为它们是球形测地线,即球体上的直线(类似于飞机飞行的路线)
层次结构中的每个单元格都有一个 level 级别,定义为单元格细分的次数(以面单元格开始)。细胞水平范围从 0 到 30。在 level - 30 的最小细胞被称为叶细胞,总共有6 * 4^30^个,每个在地球表面 1cm 左右。 (每个级别的单元格大小的细节可以在S2 Cell ID 数据结构找到)
S2 Level 对于空间索引和将区域逼近为单元集合非常有用。Cell 可用于表示点和区域:点通常表示为叶子节点,而区域表示为任何 Level 的 Cell 的集合。例如,下面是夏威夷近似的22个单元的集合:
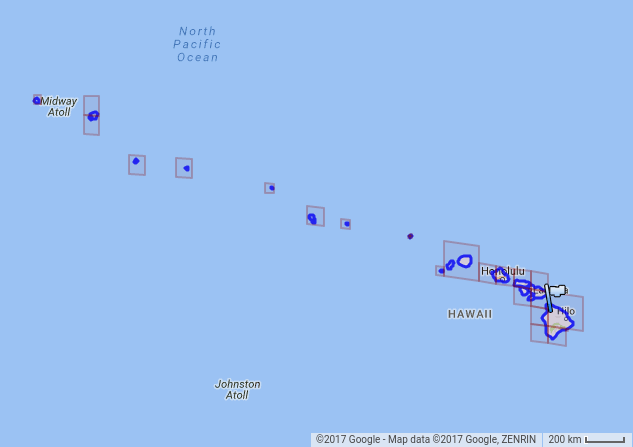
二. S(lat,lng) -> f(x,y,z)
纬度 Latitude 的取值范围在 [-90°,90°] 之间。
经度 Longitude 的取值范围在 [-180°,180°] 之间。
第一步转换,将球面坐标转换成三维直角坐标
func makeCell() {
latlng := s2.LatLngFromDegrees(30.64964508, 104.12343895)
cellID := s2.CellIDFromLatLng(latlng)
}
上面短短两句话就构造了一个 64 位的CellID。
func LatLngFromDegrees(lat, lng float64) LatLng {
return LatLng{s1.Angle(lat) * s1.Degree, s1.Angle(lng) * s1.Degree}
}
上面这一步是把经纬度转换成弧度。由于经纬度是角度,弧度转角度乘以 π / 180° 即可。
const (
Radian Angle = 1
Degree = (math.Pi / 180) * Radian
}
LatLngFromDegrees 就是把经纬度转换成 LatLng 结构体。LatLng 结构体定义如下:
type LatLng struct {
Lat, Lng s1.Angle
}
得到了 LatLng 结构体以后,就可以通过 CellIDFromLatLng 方法把经纬度弧度转成 64 位的 CellID 了。
func CellIDFromLatLng(ll LatLng) CellID {
return cellIDFromPoint(PointFromLatLng(ll))
}
上述方法也分了2步完成,先把经纬度转换成坐标系上的一个点,再把坐标系上的这个点转换成 CellID。
关于经纬度如何转换成坐标系上的一个点,这部分的大体思路分析见笔者的这篇文章,这篇文章告诉你从代码实现的角度如何把球面坐标系上的一个点转换到四叉树上对应的希尔伯特曲线点。
func PointFromLatLng(ll LatLng) Point {
phi := ll.Lat.Radians()
theta := ll.Lng.Radians()
cosphi := math.Cos(phi)
return Point{r3.Vector{math.Cos(theta) * cosphi, math.Sin(theta) * cosphi, math.Sin(phi)}}
}
上面这个函数就是把经纬度转换成三维坐标系中的一个向量点,向量的起点是三维坐标的原点,终点为球面上转换过来的点。转换的关系如下图:
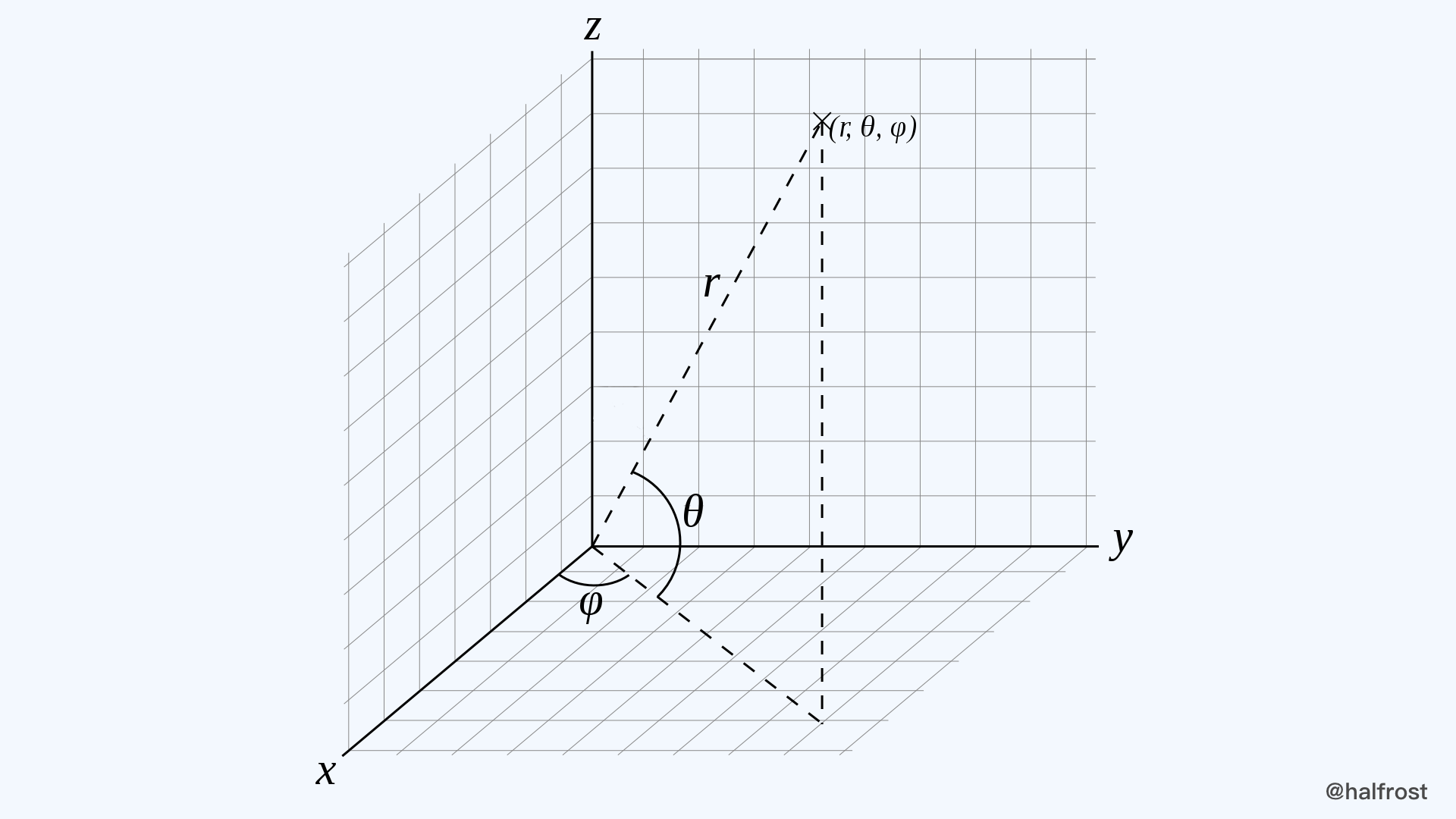
θ 即为经纬度的纬度,也就是上面代码中的 phi ,φ 即为经纬度的经度,也就是上面代码的 theta 。根据三角函数就可以得到这个向量的三维坐标:
x = r * cos θ * cos φ
y = r * cos θ * sin φ
z = r * sin θ
图中球面的半径 r = 1 。所以最终构造出来的向量即为:
r3.Vector{math.Cos(theta) * cosphi, math.Sin(theta) * cosphi, math.Sin(phi)}
(x, y, z) 为方向向量,它们并不要求是单位向量。(x, y, z) 的取值范围在 [-1,+1] x [-1,+1] x [-1,+1] 这样的立方体三维空间中。它们可以被标准化以使得在单位球上获得对应的点。
至此,已经完成了球面上的点S(lat,lng) -> f(x,y,z) 的转换。
三. f(x,y,z) -> g(face,u,v)
接下来进行 f(x,y,z) -> g(face,u,v) 的转换
func xyzToFaceUV(r r3.Vector) (f int, u, v float64) {
f = face(r)
u, v = validFaceXYZToUV(f, r)
return f, u, v
}
这里的思路是进行投影。
先从 x,y,z 三个轴上选择一个最长的轴,作为主轴。
func (v Vector) LargestComponent() Axis {
t := v.Abs()
if t.X > t.Y {
if t.X > t.Z {
return XAxis
}
return ZAxis
}
if t.Y > t.Z {
return YAxis
}
return ZAxis
}
默认定义 x 轴为0,y轴为1,z轴为2 。
const (
XAxis Axis = iota
YAxis
ZAxis
)
最后 face 的值就是三个轴里面最长的轴,注意这里限定了他们三者都在 [0,5] 之间,所以如果是负轴就需要 + 3 进行修正。实现代码如下。
func face(r r3.Vector) int {
f := r.LargestComponent()
switch {
case f == r3.XAxis && r.X < 0:
f += 3
case f == r3.YAxis && r.Y < 0:
f += 3
case f == r3.ZAxis && r.Z < 0:
f += 3
}
return int(f)
}
所以 face 的6个面上的值就确定下来了。主轴为 x 正半轴,face = 0;主轴为 y 正半轴,face = 1;主轴为 z 正半轴,face = 2;主轴为 x 负半轴,face = 3;主轴为 y 负半轴,face = 4;主轴为 z 负半轴,face = 5 。
选定主轴以后就要把另外2个轴上的坐标点投影到这个面上,具体做法就是投影或者坐标系转换。
func validFaceXYZToUV(face int, r r3.Vector) (float64, float64) {
switch face {
case 0:
return r.Y / r.X, r.Z / r.X
case 1:
return -r.X / r.Y, r.Z / r.Y
case 2:
return -r.X / r.Z, -r.Y / r.Z
case 3:
return r.Z / r.X, r.Y / r.X
case 4:
return r.Z / r.Y, -r.X / r.Y
}
return -r.Y / r.Z, -r.X / r.Z
}
上述就是 face 6个面上的坐标系转换。如果直观的对应一个外切立方体的哪6个面,那就是 face = 0 对应的是前面,face = 1 对应的是右面,face = 2 对应的是上面,face = 3 对应的是后面,face = 4 对应的是左面,face = 5 对应的是下面。
注意这里的三维坐标轴是符合右手坐标系的。即 右手4个手指沿着从 x 轴旋转到 y 轴的方向,大拇指的指向就是另外一个面的正方向。
比如立方体的前面,右手从 y 轴的正方向旋转到 z 轴的正方向,大拇指指向的是 x 轴的正方向,所以对应的就是前面。再举个例子,立方体的下面,右手从 y 轴的负方向旋转到 x 轴的负方向,大拇指指向的是 z 轴负方向,所以对应的是下面。
(face,u,v) 表示一个立方空间坐标系,三个轴的值域都是 [-1,1] 之间。为了使得每个 cell 的大小都一样,就要进行变换,具体变换规则就在下一步转换中。
四. g(face,u,v) -> h(face,s,t)
从 u、v 转换到 s、t 用的是二次变换。在 C ++ 的版本中有三种变换,至于为何最后选了这种二次变换,原因见这里。
// 线性转换
u = 0.5 * ( u + 1)
// tan() 变换
u = 2 / pi * (atan(u) + pi / 4) = 2 * atan(u) / pi + 0.5
// 二次变换
u >= 0,u = 0.5 * sqrt(1 + 3*u)
u < 0, u = 1 - 0.5 * sqrt(1 - 3*u)
在 Go 中,转换直接就只有二次变换了,其他两种变换在 Go 的实现版本中就直接没有相应的代码。
func uvToST(u float64) float64 {
if u >= 0 {
return 0.5 * math.Sqrt(1+3*u)
}
return 1 - 0.5*math.Sqrt(1-3*u)
}
(face,s,t) 表示一个 cell 空间坐标系,s,t 的值域都是 [0,1] 之间。它们代表了一个 face 上的一个 point。例如,点 (s,t) = (0.5,0.5) 代表的是在这个 face 面上的中心点。这个点也是当前这个面上再细分成4个小 cell 的顶点。
五. h(face,s,t) -> H(face,i,j)
这一部分是坐标系的转换,具体思想见这里。
将 s、t 上的点转换成坐标系 i、j 上的点。
func stToIJ(s float64) int {
return clamp(int(math.Floor(maxSize*s)), 0, maxSize-1)
}
s,t的值域是[0,1],现在值域要扩大到[0,2^30^-1]。这里只是其中一个面。
六. H(face,i,j) -> CellID
在进行最后的转换之前,先回顾一下到目前为止的转换流程。
func CellIDFromLatLng(ll LatLng) CellID {
return cellIDFromPoint(PointFromLatLng(ll))
}
func cellIDFromPoint(p Point) CellID {
f, u, v := xyzToFaceUV(r3.Vector{p.X, p.Y, p.Z})
i := stToIJ(uvToST(u))
j := stToIJ(uvToST(v))
return cellIDFromFaceIJ(f, i, j)
}
S(lat,lng) -> f(x,y,z) -> g(face,u,v) -> h(face,s,t) -> H(face,i,j) -> CellID 总共有5步转换。
经过上面5步转换以后,等效于把地球上的经纬度的点都转换到了希尔伯特曲线上的点了。

在解释最后一步转换 CellID 之前,先说明一下方向的问题。
有2个存了常量的数组:
ijToPos = [4][4]int{
{0, 1, 3, 2}, // canonical order
{0, 3, 1, 2}, // axes swapped
{2, 3, 1, 0}, // bits inverted
{2, 1, 3, 0}, // swapped & inverted
}
posToIJ = [4][4]int{
{0, 1, 3, 2}, // canonical order: (0,0), (0,1), (1,1), (1,0)
{0, 2, 3, 1}, // axes swapped: (0,0), (1,0), (1,1), (0,1)
{3, 2, 0, 1}, // bits inverted: (1,1), (1,0), (0,0), (0,1)
{3, 1, 0, 2}, // swapped & inverted: (1,1), (0,1), (0,0), (1,0)
}
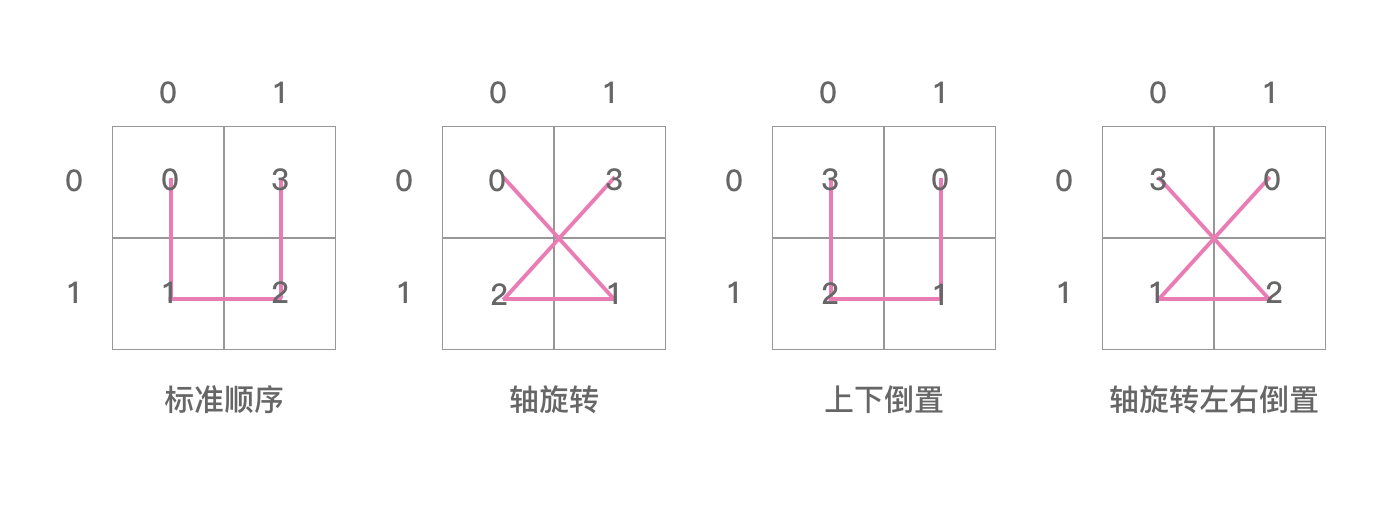
这两个二维数组里面的值用图表示出来如下两个图:
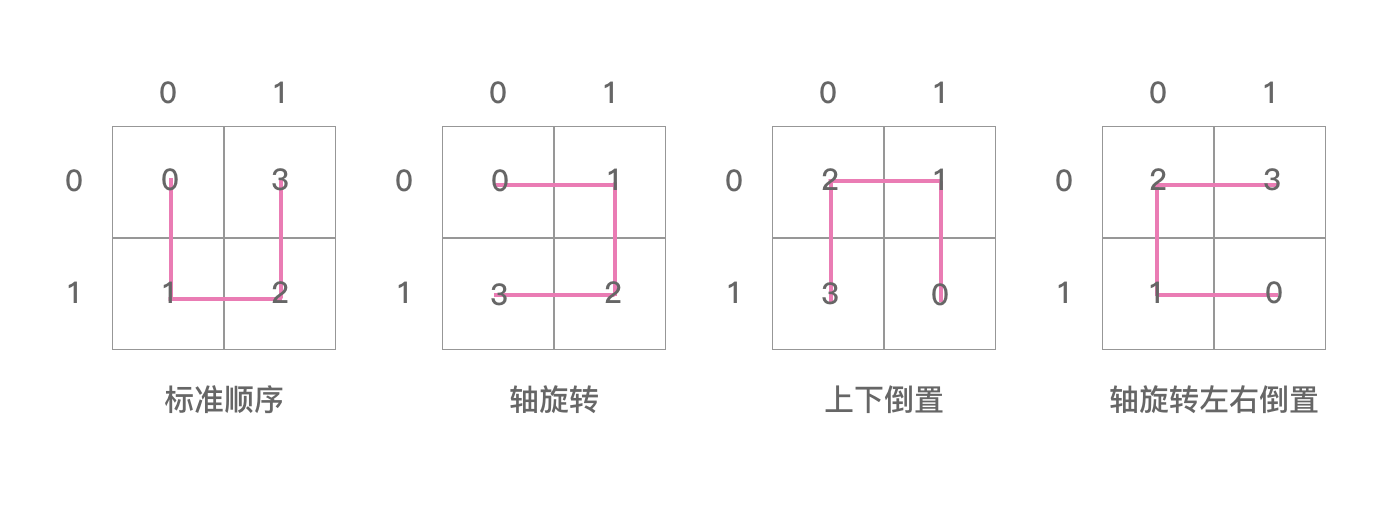
上图是 posToIJ ,注意这里的 i,j 指的是坐标值,如上图。这里是一阶的希尔伯特曲线,所以 i,j 就等于坐标轴上的值。posToIJ[0] = {0, 1, 3, 2} 表示的就是上图中图0的样子。同理,posToIJ[1] 表示的是图1,posToIJ[2] 表示的是图2,posToIJ[3] 表示的是图3 。
从上面这四张图我们可以看出:
posToIJ 的四张图其实是“ U ” 字形逆时针分别旋转90°得到的。这里我们只能看出四张图相互之间的联系,即兄弟之间的联系,但是看不到父子图相互之间的联系。
posToIJ[0] = {0, 1, 3, 2} 里面存的值是 ij 合在一起表示的值。posToIJ[0][0] = 0,指的是 i = 0,j = 0 的那个方格,ij 合在一起是00,即0。posToIJ[0][1] = 1,指的是 i = 0,j = 1 的那个方格,ij 合在一起是01,即1。posToIJ[0][2] = 1,指的是 i = 1,j = 1 的那个方格,ij 合在一起是11,即3。posToIJ[0][3] = 2,指的是 i = 1,j = 0 的那个方格,ij 合在一起是10,即2。数组里面的顺序是 “ U ” 字形画的顺序。所以 posToIJ[0] = {0, 1, 3, 2} 表示的是图0中的样子。其他图形同理。
这上面的四张图是 ijToPos 数组。这个数组在整个库中也没有被用到,这里不用关系它对应的关系。
初始化 lookupPos 数组和 lookupIJ 数组 由如下的代码实现的。
func init() {
initLookupCell(0, 0, 0, 0, 0, 0)
initLookupCell(0, 0, 0, swapMask, 0, swapMask)
initLookupCell(0, 0, 0, invertMask, 0, invertMask)
initLookupCell(0, 0, 0, swapMask|invertMask, 0, swapMask|invertMask)
}
我们把变量的值都代进去,代码就会变成下面的样子:
func init() {
initLookupCell(0, 0, 0, 0, 0, 0)
initLookupCell(0, 0, 0, 1, 0, 1)
initLookupCell(0, 0, 0, 2, 0, 2)
initLookupCell(0, 0, 0, 3, 0, 3)
}
initLookupCell 入参有6个参数,有4个参数都是0,我们需要重点关注的是第四个参数和第六个参数。第四个参数是 origOrientation,第六个参数是 orientation。
进入到 initLookupCell 方法中,有如下的4行:
initLookupCell(level, i+(r[0]>>1), j+(r[0]&1), origOrientation, pos, orientation^posToOrientation[0])
initLookupCell(level, i+(r[1]>>1), j+(r[1]&1), origOrientation, pos+1, orientation^posToOrientation[1])
initLookupCell(level, i+(r[2]>>1), j+(r[2]&1), origOrientation, pos+2, orientation^posToOrientation[2])
initLookupCell(level, i+(r[3]>>1), j+(r[3]&1), origOrientation, pos+3, orientation^posToOrientation[3])
这里顺带说一下 r[0]>>1 和 r[0]&1 究竟做了什么。
r := posToIJ[orientation]
r 数组来自于 posToIJ 数组。posToIJ 数组上面说过了,它里面装的其实是4个不同方向的“ U ”字。相当于表示了当前四个小方格兄弟相互之间的方向。r[0]、r[1]、r[2]、r[3] 取出的其实就是 00,01,10,11 这4个数。那么 r[0]>>1 操作就是取出二位二进制位的前一位,即 i 位。r[0]&1 操作就是取出二位二进制位的后一位,即 j 位。r[1]、r[2]、r[3] 同理。
再回到方向的问题上来。需要优先说明的是下面4行干了什么。
orientation^posToOrientation[0]
orientation^posToOrientation[1]
orientation^posToOrientation[2]
orientation^posToOrientation[3]
再解释之前,先让我们看看 posToOrientation 数组:
posToOrientation = [4]int{swapMask, 0, 0, invertMask | swapMask}
把数值代入到上面数组中:
posToOrientation = [4]int{1, 0, 0, 3}
posToOrientation 数组里面装的原始的值是 [01,00,00,11],这个4个数值并不是随便初始化的。
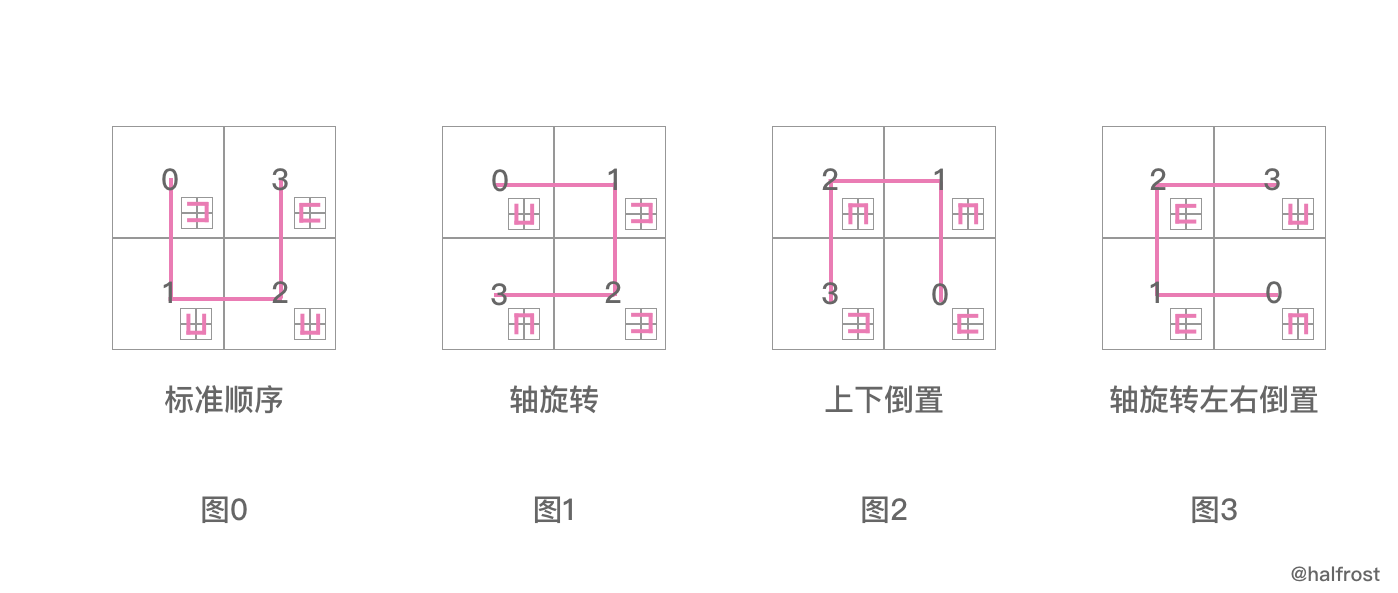
其实这个对应的就是 图0 中4个小方块接下来再划分的方向。图0 中0号的位置下一个图的方向应该是图1,即01;图0 中1号的位置下一个图的方向应该是图0,即00;图0 中2号的位置下一个图的方向应该是图0,即00;图0 中3号的位置下一个图的方向应该是图3,即11 。这就是初始化 posToOrientation 数组里面的玄机了。
posToIJ 的四张图我们只能看出兄弟之间的关系,那么 posToOrientation 的四张图让我们知道了父子之间的关系。
回到上面说的代码:
orientation^posToOrientation[0]
orientation^posToOrientation[1]
orientation^posToOrientation[2]
orientation^posToOrientation[3]
每次 orientation 都异或 posToOrientation 数组。这样就能保证每次都能根据上一次的原始的方向推算出当前的 pos 所在的方向。即计算父子之间关系。
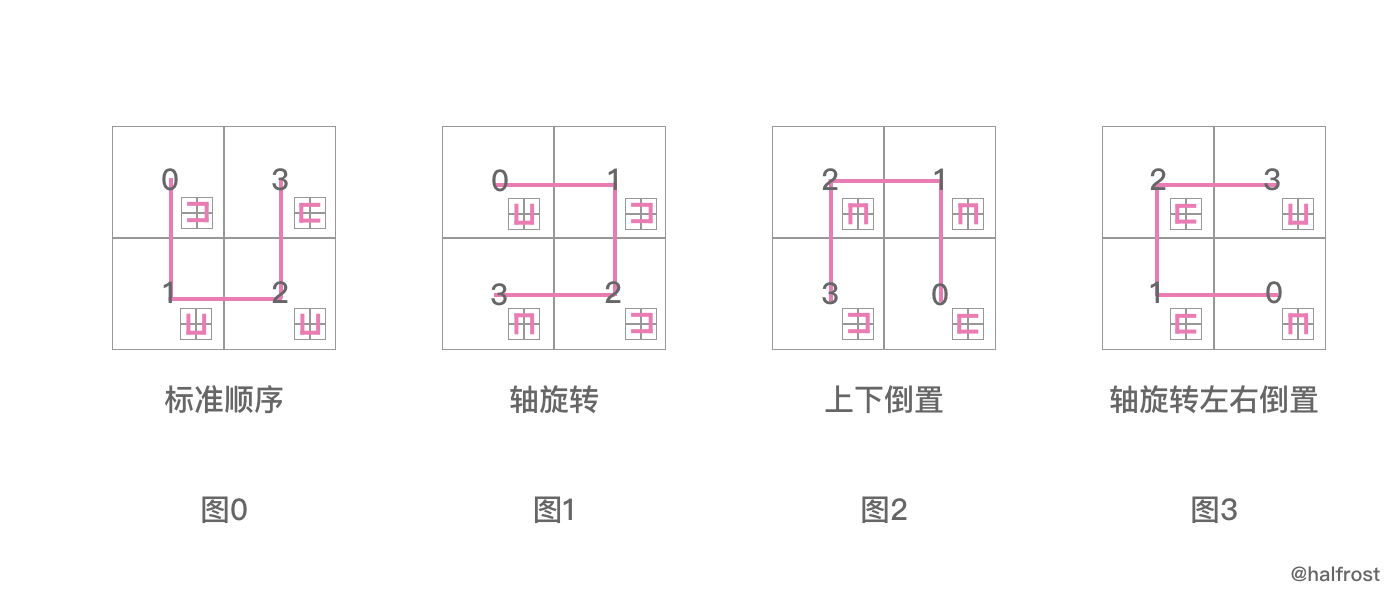
还是回到这张图上来。兄弟之间的关系是逆时针旋转90°的关系。那这4个兄弟都作为父亲,分别和各自的4个孩子之间什么关系呢?结论是,**父子之间的关系都是 01,00,00,11 的关系。**从图上我们也可以看出这一点,图1中,“ U ” 字形虽然逆时针旋转了90°,但是它们的孩子也跟着旋转了90°(相对于图0来说)。图2,图3也都如此。
用代码表示这种关系,就是下面这4行代码
orientation^posToOrientation[0]
orientation^posToOrientation[1]
orientation^posToOrientation[2]
orientation^posToOrientation[3]
举个例子,假设 orientation = 0,即图0,那么:
00 ^ 01 = 01
00 ^ 00 = 00
00 ^ 00 = 00
00 ^ 11 = 11
图0 的四个孩子的方向就被我们算出来了,01,00,00,11,1003 。和上面图片中图0展示的是一致的。
orientation = 1,orientation = 2,orientation = 3,都是同理的:
01 ^ 01 = 00
01 ^ 00 = 01
01 ^ 00 = 01
01 ^ 11 = 10
10 ^ 01 = 11
10 ^ 00 = 10
10 ^ 00 = 10
10 ^ 11 = 01
11 ^ 01 = 10
11 ^ 00 = 11
11 ^ 00 = 11
11 ^ 11 = 00
图1孩子的方向是0,1,1,2 。图2孩子的方向是3,2,2,1 。图3孩子的方向是2,3,3,0 。和图上画的是完全一致的。
所以上面的转换是很关键的。这里就是针对希尔伯特曲线的父子方向进行换算的。
最后会有读者有疑问,origOrientation 和 orientation 是啥关系?
lookupPos[(ij<<2)+origOrientation] = (pos << 2) + orientation
lookupIJ[(pos<<2)+origOrientation] = (ij << 2) + orientation
数组下标里面存的都是 origOrientation,下标里面存的值都是 orientation。
解释完希尔伯特曲线方向的问题之后,接下来可以再仔细说说 55 的坐标转换的问题。前一篇文章《高效的多维空间点索引算法 — Geohash 和 Google S2》里面有谈到这个问题,读者有些疑惑点,这里再最终解释一遍。
在 Google S2 中,初始化 initLookupCell 的时候,会初始化2个数组,一个是 lookupPos 数组,一个是 lookupIJ 数组。中间还会用到 i , j , pos 和 orientation 四个关键的变量。orientation 这个之前说过了,这里就不再赘述了。需要详细说明的 i ,j 和 pos 的关系。
pos 指的是在 希尔伯特曲线上的位置。这个位置是从 希尔伯特 曲线的起点开始算的。从起点开始数,到当前是第几块方块。注意这个方块是由 4 个小方块组成的大方块。因为 orientation 是选择4个方块中的哪一个。
在 55 的这个例子里,pos 其实是等于 13 的。代表当前4块小方块组成的大方块是距离起点的第13块大方块。由于每个大方块是由4个小方块组成的。所以当前这个大方块的第一个数字是 13 * 4 = 52 。代码实现就是左移2位,等价于乘以 4 。再加上 55 的偏移的 orientation = 11,再加 3 ,所以 52 + 3 = 55 。
再说说 i 和 j 的问题,在 55 的这个例子里面 i = 14,1110,j = 13,1101 。如果直观的看坐标系,其实 55 是在 (5,2) 的坐标上。但是现在为何 i = 14,j = 13 呢 ?这里容易弄混的就是 i ,j 和 pos 的关系。
注意:
i,j 并不是直接对应的 希尔伯特曲线 坐标系上的坐标。因为初始化需要生成的是五阶希尔伯特曲线。在 posToIJ 数组表示的一阶希尔伯特曲线,所以 i,j 才直接对应的 希尔伯特曲线 坐标系上的坐标。
读者到这里就会疑问了,那是什么参数对应的是希尔伯特曲线坐标系上的坐标呢?
pos 参数对应的就是希尔伯特曲线坐标系上的坐标。一旦一个希尔伯特曲线的起始点和阶数确定以后,四个小方块组成的一个大方块的 pos 位置确定以后,那么它的坐标其实就已经确定了。希尔伯特曲线上的坐标并不依赖 i,j,完全是由曲线的性质和 pos 位置决定的。
我们并不关心希尔伯特曲线上小方块的坐标,我们关心的是 pos 和 i,j 的转换关系!
疑问又来了,那 i,j 对应的是什么坐标系上的坐标呢?
i,j 对应的是一个经过坐标变换以后的坐标系坐标。
我们知道,在进行 ( u,v ) -> ( i,j ) 变换的时候,u,v 的值域是 [0,1] 之间,然后经过变换要变到 [ 0, 2^30^-1 ] 之间。i,j 就是变换以后坐标系上的坐标值,i,j 的值域变成了 [ 0, 2^30^-1 ] 。
那初始化计算 lookupPos 数组和 lookupIJ 数组有什么用呢?这两个数组就是把 i,j 和 pos 联系起来的数组。知道 pos 以后可以立即找到对应的 i,j。知道 i,j 以后可以立即找到对应的 pos。
i,j 和 pos 互相转换之间的桥梁就是生成希尔伯特曲线的方式。这种方式可以类比 Z - index 曲线的生成方式。
Z - index 曲线的生成方式是把经纬度坐标分别进行区间二分,在左区间的记为0,在右区间的记为1 。将这两串二进制字符串偶数位放经度,奇数位放纬度,最终组合成新的二进制串,这个串再经过 base-32 编码以后,最终就生成了 geohash 。
那么 希尔伯特 曲线的生成方式是什么呢?它先将经纬度坐标转换成了三维直角坐标系坐标,然后再投影到外切立方体的6个面上,于是三维直角坐标系坐标 (x,y,z) 就转换成了 (face,u,v) 。 (face,u,v) 经过一个二次变换变成 (face,s,t) , (face,s,t) 经过坐标系变换变成了 (face,i,j) 。然后将 i,j 分别4位4位的取出来,i 的4位二进制位放前面,j 的4位二进制位放后面。最后再加上希尔伯特曲线的方向位 orientation 的2位。组成 iiii jjjj oo 类似这样的10位二进制位。通过 lookupPos 数组这个桥梁,找到对应的 pos 的值。pos 的值就是对应希尔伯特曲线上的位置。然后依次类推,再取出 i 的4位,j 的4位进行这样的转换,直到所有的 i 和 j 的二进制都取完了,最后把这些生成的 pos 值安全先生成的放在高位,后生成的放在低位的方式拼接成最终的 CellID。
这里可能有读者疑问了,为何要 iiii jjjj oo 这样设计,为何是4位4位的,谷歌开发者在注释里面这样写道:“我们曾经考虑过一次组合 16 位,14位的 position + 2位的 orientation,但是代码实际运行起来发现小数组拥有更好的性能,2KB 更加适合存储到主 cache 中。”
在 Google S2 中,i,j 每次转换都是4位,所以 i,j 的有效值取值是 0 - 15,所以 iiii jjjj oo 是一个十进制的数,能表示的范围是 2^10^ = 1024 。那么 pos 初始化值也需要计算到 1024 。由于 pos 是4个小方块组成的大方块,它本身就是一个一阶的希尔伯特曲线。所以初始化需要生成一个五阶的希尔伯特曲线。

上图是一阶的希尔伯特曲线。是由4个小方格组成的。

上图是二阶的希尔伯特曲线,是由4个 pos 方格组成的。
上图是三阶的希尔伯特曲线。

上图是四阶的希尔伯特曲线。

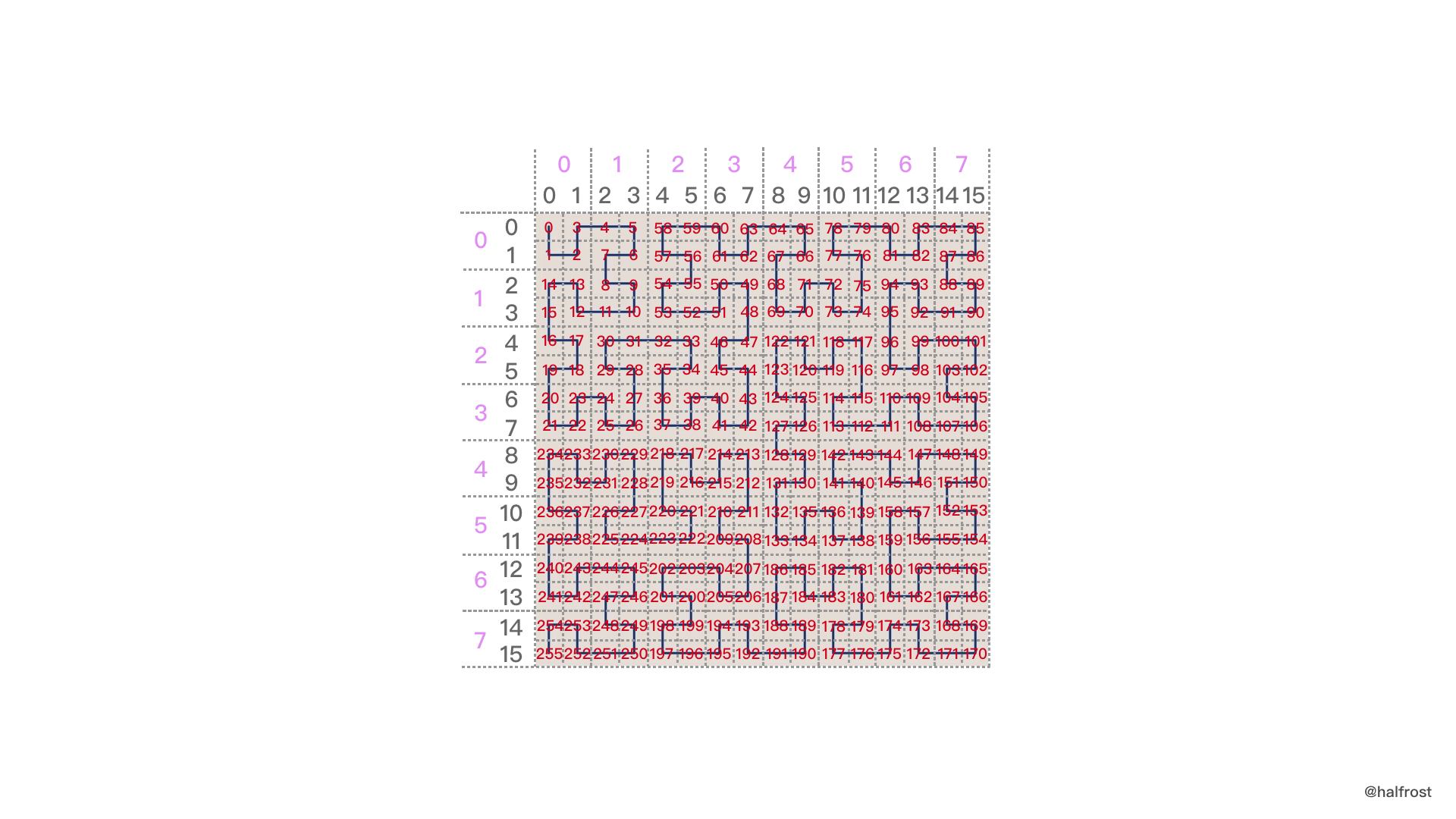
上图是五阶的希尔伯特曲线。pos 方格总共有1024个。
至此已经说清楚了希尔伯特曲线的方向和在 Google S2 中生成希尔伯特曲线的阶数,五阶希尔伯特曲线。
由此也可以看出,希尔伯特曲线的是由 “ U ” 字形构成的,由4个不同方向的 “ U ” 字构成。初始方向是开口朝上的 “ U ”。
关于希尔伯特曲线生成的动画,见上篇《高效的多维空间点索引算法 — Geohash 和 Google S2》—— 希尔伯特曲线的构造方法 这一章节。
那么现在我们再推算55就比较简单了。从五阶希尔伯特曲线开始推,推算过程如下图。
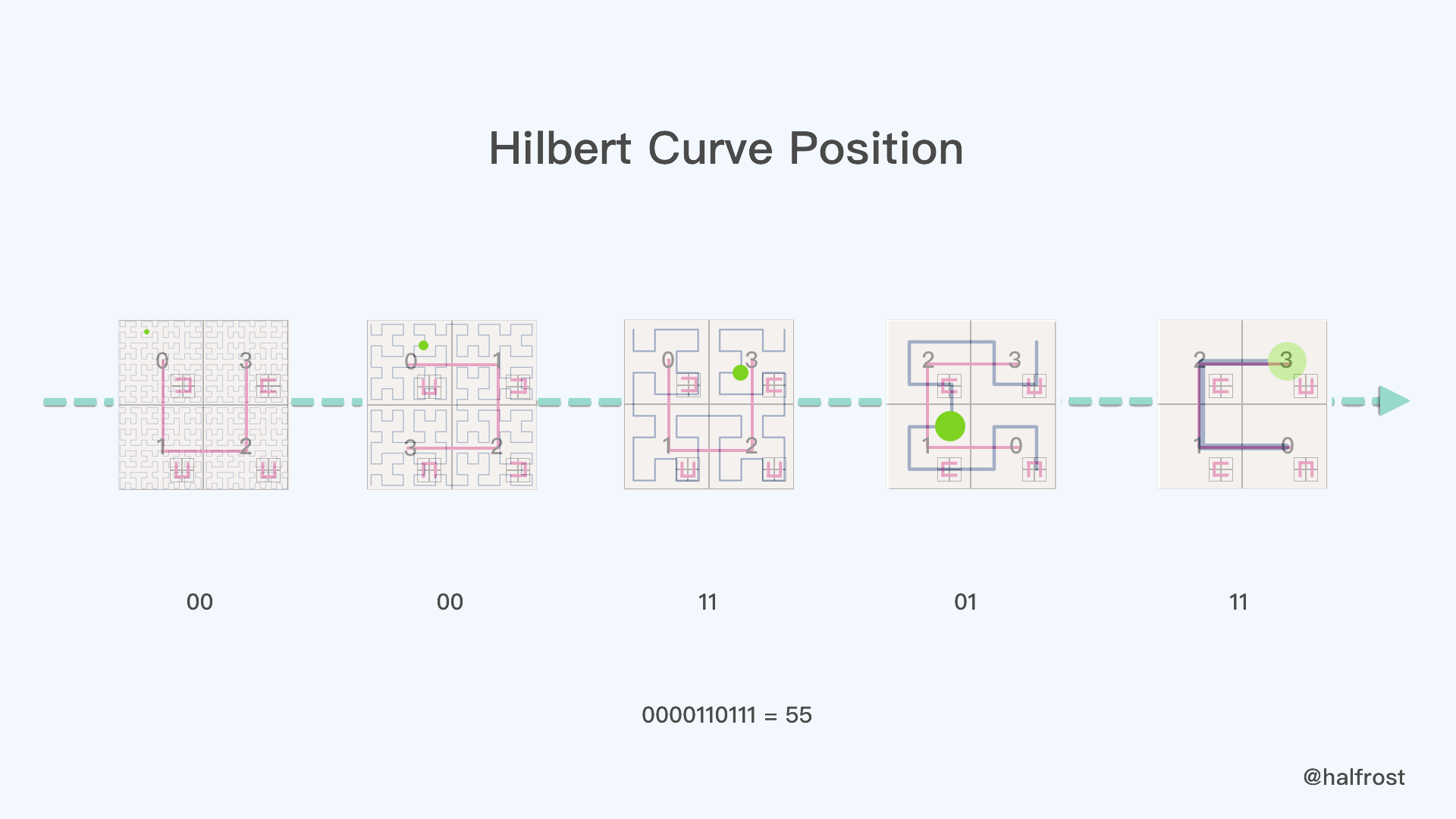
首先55是在上图中每个小图中绿色点的位置。我们不断的进行方向的判断。第一张小图,绿点在00的位置。第二张小图,绿点在00的位置。第三张小图,绿点在11的位置。第四张小图,绿点在01的位置。第五张小图,绿点在11的位置。其实换算到第四步,得到的数值就是 pos 的值,即 00001101 = 13 。最后2位是具体的点在 pos 方格里面的位置,是11,所以 13 * 4 + 3 = 55 。
当然直接根据方向推算到底,也可以得到 0000110111 = 55 ,同样也是55 。
七. 举例
最后举个具体的完整的例子:
由于 Ghost 不支持表格,所以这里的表格请见我的 GitHub
上面完成了前4步的转换。
最后一步转换成 CellID 。具体实现代码如下。由于 CellID 是64位的,除去 face 占的3位,最后一个标志位 1 占的位置,剩下 60 位。
func cellIDFromFaceIJ(f, i, j int) CellID {
// 1.
n := uint64(f) << (posBits - 1)
// 2.
bits := f & swapMask
// 3.
for k := 7; k >= 0; k-- {
mask := (1 << lookupBits) - 1
bits += int((i>>uint(k*lookupBits))&mask) << (lookupBits + 2)
bits += int((j>>uint(k*lookupBits))&mask) << 2
bits = lookupPos[bits]
// 4.
n |= uint64(bits>>2) << (uint(k) * 2 * lookupBits)
// 5.
bits &= (swapMask | invertMask)
}
// 6.
return CellID(n*2 + 1)
}
具体步骤如下:
- 将 face 左移 60 位。
- 计算初始的 origOrientation。初始的 origOrientation 是 face 转换得来的,face & 01 以后的结果是为了使每个面都有一个右手坐标系。
- 循环,从头开始依次取出 i ,j 的4位二进制位,计算出 ij<<2 + origOrientation,然后查 lookupPos 数组找到对应的 pos<<2 + orientation 。
- 拼接 CellID,右移 pos<<2 + orientation 2位,只留下 pos ,把pos 继续拼接到 上次循环的 CellID 后面。
- 计算下一个循环的 origOrientation。&= (swapMask | invertMask) 即 & 11,也就是取出末尾的2位二进制位。
- 最后拼接上最后一个标志位 1 。
这里说说第二步,origOrientation 的转换。
我们知道 face 是有6个面的,编号依次是 000,001,010,011,100,101 。想让这6个面都具有右手坐标系的性质,就必须进行转换,转换的规则其实进行一次位运算即可:
000 & 001 = 00
001 & 001 = 01
010 & 001 = 00
011 & 001 = 01
100 & 001 = 00
101 & 001 = 01
经过转换以后,face & 01 的值就是初始的 origOrientation 了。
用表展示出每一步(表比较长,请右滑):
由于 Ghost 不支持表格,所以这里的表格请见我的 GitHub
任意取出循环中的一个情况,用图表示如下:

注意:由于 CellID 是64位的,头三位是 face ,末尾一位是标志位,所以中间有 60 位。i,j 转换成二进制是30位的。7个4位二进制位和1个2位二进制位。4*7 + 2 = 30 。iijjoo ,即 i 的头2个二进制位和 j 的头2个二进制位加上 origOrientation,这样组成的是6位二进制位,最多能表示 2^6^ = 32,转换出来的 pos + orientation 最多也是32位的。即转换出来最多也是6位的二进制位,除去末尾2位 orientation ,所以 pos 在这种情况下最多是 4位。iiiijjjjpppp,即 i 的4个二进制位和 j 的4个二进制位加上 origOrientation,这样组成的是10位二进制位,最多能表示 2^10^ = 1024,转换出来的 pos + orientation 最多也是10位的。即转换出来最多也是10位的二进制位,除去末尾2位 orientation ,所以 pos 在这种情况下最多是 8位。
由于最后 CellID 只拼接 pos ,所以 4 + 7 * 8 = 60 位。拼接完成以后,中间的60位都由 pos 组成的。最后拼上头3位,末尾的1位标志位,64位的 CellID 就这样生成了。
到此,所有的 CellID 生成过程就结束了。
空间搜索系列文章:
如何理解 n 维空间和 n 维时空
高效的多维空间点索引算法 — Geohash 和 Google S2
Google S2 中的 CellID 是如何生成的 ?
Google S2 中的四叉树求 LCA 最近公共祖先
神奇的德布鲁因序列
GitHub Repo:Halfrost-Field
Follow: halfrost · GitHub





