关于邻居的定义,相邻即为邻居,那么邻居分为2种,边相邻和点相邻。边相邻的有4个方向,上下左右。点相邻的也有4个方向,即4个顶点相邻的。
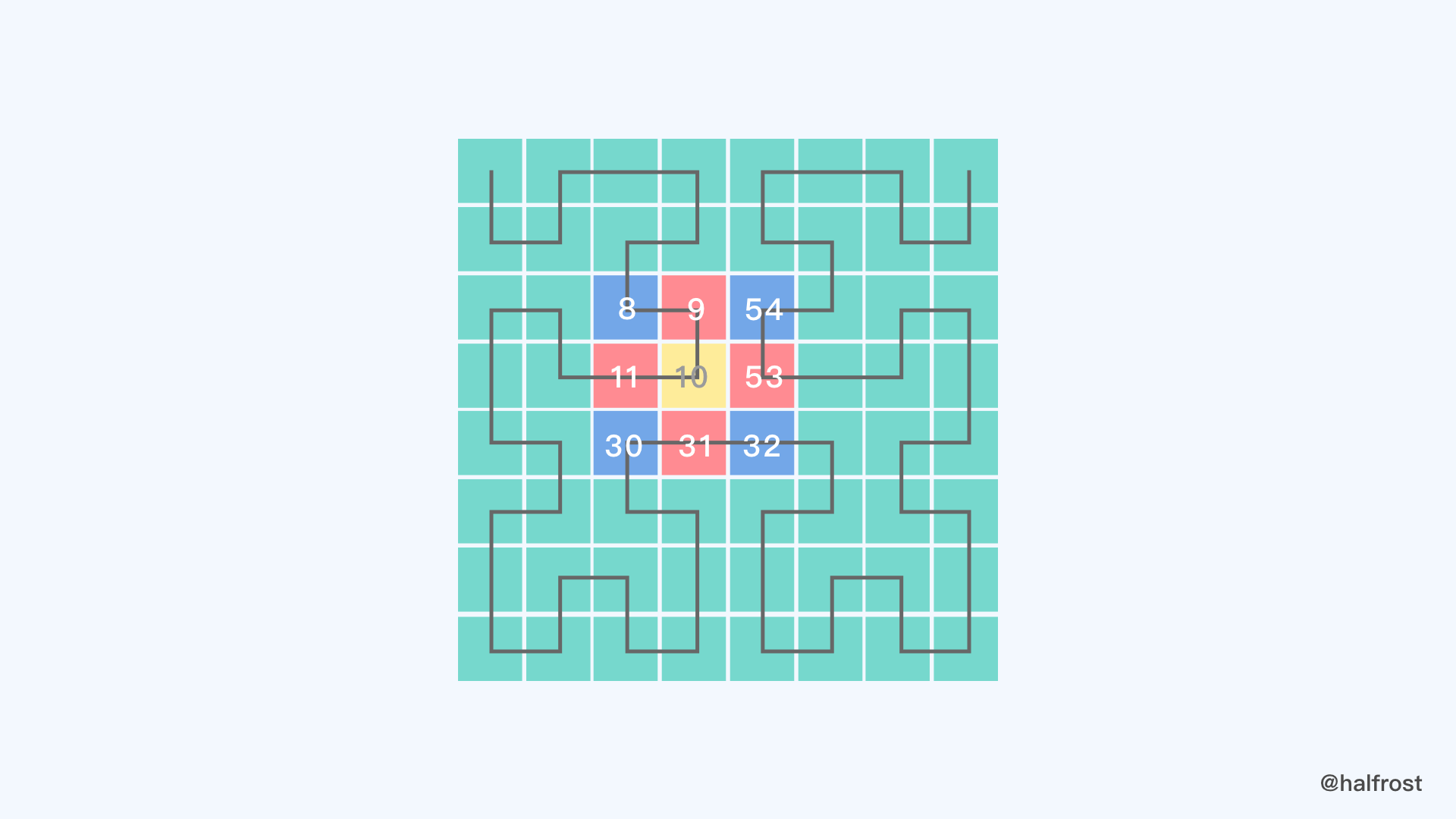
如上图,绿色的区域是一颗四叉树表示的范围,四叉树上面有一个点,图中黄色区域标明的点。现在想求四叉树上黄色的点的希尔伯特曲线邻居。图中黑色的线就是一颗穿过四叉树的希尔伯特曲线。希尔伯特曲线的起点0在左上角的方格中,终点63在右上角的方格中。
红色的四个格子是黄色格子边相邻邻居,蓝色的四个格子是黄色格子的顶点相邻的邻居,所以黄色格子的邻居为8个格子,分别表示的点是8,9,54,11,53,30,31,32 。可以看出来这些邻居在表示的点上面并不是相邻的。
那么怎么求四叉树上任意一点的希尔伯特曲线邻居呢?
一. 边邻居
边邻居最直接的想法就是 先拿到中心点的坐标 (i,j) ,然后通过坐标系的关系,拿到与它边相邻的 Cell 的坐标 (i + 1,j) , (i - 1,j) , (i,j - 1) , (i,j + 1) 。
实际做法也是如此。不过这里涉及到需要转换的地方。这里需要把希尔伯特曲线上的点转换成坐标以后才能按照上面的思路来计算边邻居。
关于 CellID 的生成与数据结构,见笔者这篇《Google S2 中的 CellID 是如何生成的 ?》
按照上述的思路,实现出来的代码如下:
func (ci CellID) EdgeNeighbors() [4]CellID {
level := ci.Level()
size := sizeIJ(level)
f, i, j, _ := ci.faceIJOrientation()
return [4]CellID{
cellIDFromFaceIJWrap(f, i, j-size).Parent(level),
cellIDFromFaceIJWrap(f, i+size, j).Parent(level),
cellIDFromFaceIJWrap(f, i, j+size).Parent(level),
cellIDFromFaceIJWrap(f, i-size, j).Parent(level),
}
}
边按照,下边,右边,上边,左边,逆时针的方向依次编号0,1,2,3 。
接下来具体分析一下里面的实现。
func sizeIJ(level int) int {
return 1 << uint(maxLevel-level)
}
sizeIJ 保存的是当前 Level 的格子边长大小。这个大小是相对于 Level 30 来说的。比如 level = 29,那么它的 sizeIJ 就是2,代表 Level 29 的一个格子边长是由2个 Level 30 的格子组成的,那么也就是2^2^=4个小格子组成的。如果是 level = 28,那么边长就是4,由16个小格子组成。其他都以此类推。
func (ci CellID) faceIJOrientation() (f, i, j, orientation int) {
f = ci.Face()
orientation = f & swapMask
nbits := maxLevel - 7*lookupBits // first iteration
for k := 7; k >= 0; k-- {
orientation += (int(uint64(ci)>>uint64(k*2*lookupBits+1)) & ((1 << uint((2 * nbits))) - 1)) << 2
orientation = lookupIJ[orientation]
i += (orientation >> (lookupBits + 2)) << uint(k*lookupBits)
j += ((orientation >> 2) & ((1 << lookupBits) - 1)) << uint(k*lookupBits)
orientation &= (swapMask | invertMask)
nbits = lookupBits // following iterations
}
// 下面这个判断详细解释
if ci.lsb()&0x1111111111111110 != 0 {
orientation ^= swapMask
}
return
}
这个方法就是把 CellID 再分解回原来的 i 和 j。这里具体的过程在笔者这篇《Google S2 中的 CellID 是如何生成的 ?》里面的 cellIDFromFaceIJ 方法里面有详细的叙述,这里就不再赘述了。cellIDFromFaceIJ 方法和 faceIJOrientation 方法是互为逆方法。
cellIDFromFaceIJ 是把 face,i,j 这个当入参传进去,返回值是 CellID,faceIJOrientation 是把 CellID 分解成 face,i,j,orientation。faceIJOrientation 比 cellIDFromFaceIJ 分解出来多一个 orientation。
这里需要重点解释的是 orientation 怎么计算出来的。
我们知道 CellID 的数据结构是 3位 face + 60位 position + 1位标志位。那么对于 Level - n 的非叶子节点,3位 face 之后,一定是有 2 * n 位二进制位,然后紧接着 2*(maxLevel - n) + 1 位以1开头的,末尾都是0的二进制位。maxLevel = 30 。
例如 Level - 16,中间一定是有32位二进制位,然后紧接着 2*(30 - 16) + 1 = 29位。这29位是首位为1,末尾为0组成的。3 + 32 + 29 = 64 位。64位 CellID 就这样组成的。
当 n = 30,3 + 60 + 1 = 64,所以末尾的1并没有起任何作用。当 n = 29,3 + 58 + 3 = 64,于是末尾一定是 100 组成的。10对方向并不起任何作用,最后多的一个0也对方向不起任何作用。关键就是看10和0之间有多少个00 。当 n = 28,3 + 56 + 5 = 64,末尾5位是 10000,在10和0之间有一个“00”。“00”是会对方向产生影响,初始的方向应该再异或 01 才能得到。
关于 “00” 会对原始的方向产生影响,这点其实比较好理解。CellID 从最先开始的方向进行四分,每次四分都将带来一次方向的变换。直到变换到最后一个4个小格子的时候,方向就不会变化了,因为在4个小格子之间就可以唯一确定是哪一个 Cell 被选中。所以这也是上面看到了, Level - 30 和 Level - 29 的方向是不变的,除此以外的 Level 是需要再异或一次 01 ,变换以后得到原始的 orientation。
最后进行转换,具体代码实现如下:
func cellIDFromFaceIJWrap(f, i, j int) CellID {
// 1.
i = clamp(i, -1, maxSize)
j = clamp(j, -1, maxSize)
// 2.
const scale = 1.0 / maxSize
limit := math.Nextafter(1, 2)
u := math.Max(-limit, math.Min(limit, scale*float64((i<<1)+1-maxSize)))
v := math.Max(-limit, math.Min(limit, scale*float64((j<<1)+1-maxSize)))
// 3.
f, u, v = xyzToFaceUV(faceUVToXYZ(f, u, v))
return cellIDFromFaceIJ(f, stToIJ(0.5*(u+1)), stToIJ(0.5*(v+1)))
}
转换过程总共分为三步。第一步先处理 i,j 边界的问题。第二步,将 i,j 转换成 u,v 。第三步,u,v 转 xyz,再转回 u,v,最后转回 CellID 。
第一步:
func clamp(x, min, max int) int {
if x < min {
return min
}
if x > max {
return max
}
return x
}
clamp 函数就是用来限定 i , j 的范围的。i,j 的范围始终限定在 [-1,maxSize] 之间。
第二步:
最简单的想法是将(i,j)坐标转换为(x,y,z)(这个点不在边界上),然后调用 xyzToFaceUV 方法投影到对应的 face 上。
我们知道在生成 CellID 的时候,stToUV 的时候,用的是一个二次变换:
func stToUV(s float64) float64 {
if s >= 0.5 {
return (1 / 3.) * (4*s*s - 1)
}
return (1 / 3.) * (1 - 4*(1-s)*(1-s))
}
但是此处,我们用的变换就简单一点,用的是线性变换。
u = 2 * s - 1
v = 2 * t - 1
u,v 的取值范围都被限定在 [-1,1] 之间。具体代码实现:
const scale = 1.0 / maxSize
limit := math.Nextafter(1, 2)
u := math.Max(-limit, math.Min(limit, scale*float64((i<<1)+1-maxSize)))
v := math.Max(-limit, math.Min(limit, scale*float64((j<<1)+1-maxSize)))
第三步:找到叶子节点,把 u,v 转成 对应 Level 的 CellID。
f, u, v = xyzToFaceUV(faceUVToXYZ(f, u, v))
return cellIDFromFaceIJ(f, stToIJ(0.5*(u+1)), stToIJ(0.5*(v+1)))
这样就求得了一个 CellID 。
由于边有4条边,所以边邻居有4个。
return [4]CellID{
cellIDFromFaceIJWrap(f, i, j-size).Parent(level),
cellIDFromFaceIJWrap(f, i+size, j).Parent(level),
cellIDFromFaceIJWrap(f, i, j+size).Parent(level),
cellIDFromFaceIJWrap(f, i-size, j).Parent(level),
}
上面数组里面分别会装入当前 CellID 的下边邻居,右边邻居,上边邻居,左边邻居。
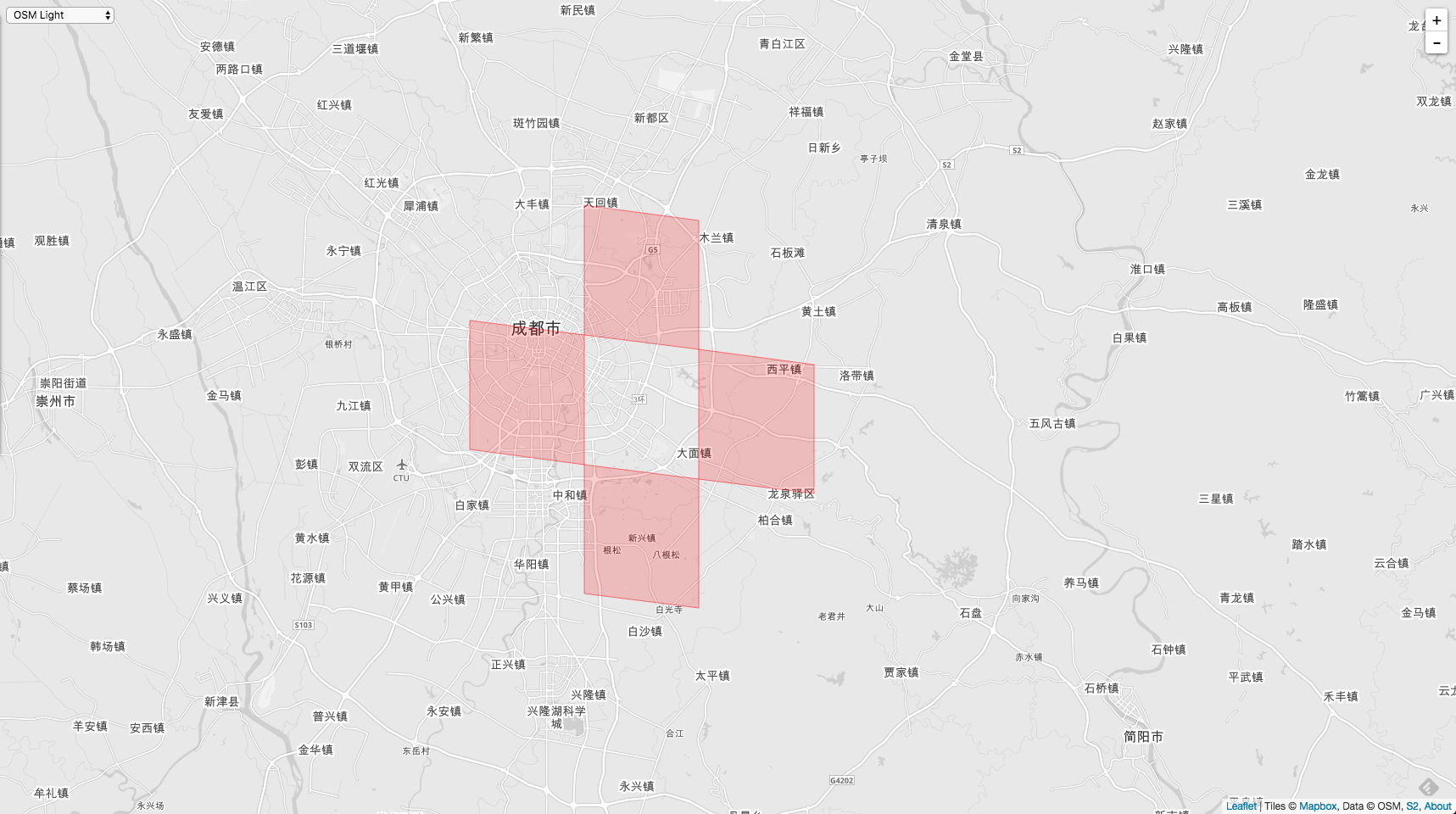
如果在地图上显示出来的话,就是下图的这样子。
中间方格的 CellID = 3958610196388904960 , Level 10 。按照上面的方法求出来的边邻居,分别是:
3958603599319138304 // 下边邻居
3958607997365649408 // 右边邻居
3958612395412160512 // 上边邻居
3958599201272627200 // 左边邻居
在地图上展示出来:
二. 共顶点邻居
这里的共顶点邻居和文章开始讲的顶点邻居有点区别。并且下面还会有一些看似奇怪的例子,也是笔者在实际编码中踩过的坑,分享一下。
这里先说明一种特殊情况,即 Cell 正好在地球的外切立方体的8个顶点上。那么这个点的顶点邻居只有3个,而不是4个。因为这8个顶点每个点只有3个面与其连接,所以每个面上有且只有一个 Cell 是它们的顶点邻居。除去这8个点以外的 Cell 的顶点邻居都有4个!
j
|
| (0,1) (1,1)
| (0,0) (1,0)
|
---------------> i
在上述的坐标轴中,i 轴方向如果为1,就落在4个象限的右边一列上。如果 j 轴方向如果为,就落在4个象限的上面一行上。
假设 Cell Level 不等于 30,即末尾标志位1后面还有0,那么这种 Cell 转换成 i,j 以后,i,j 的末尾就都是1 。
上面的结论可以证明的,因为在 faceIJOrientation 函数拆分 Cell 的时候,如果遇到了都是0的情况,比如 orientation = 11,Cell 末尾都是0,那么取出末尾8位加上orientation,00000000 11,经过 lookupIJ 转换以后得到 1111111111 ,于是 i = 1111,j = 1111 ,方向还是 11。Cell 末尾的00还是继续循环上述的过程,于是 i,j 末尾全是1111 了。
所以我们只需要根据 i,j 判断入参给的 Level 在哪个象限,就可以把共顶点的邻居都找到。
假设入参给定的 Level 小,即 Cell 的面积大,那么就需要判断当前 Cell (函数调用者) 的共顶点是位于入参 Cell 的4个顶点的哪个顶点上。Cell 是一个矩形,有4个顶点。当前 Cell (函数调用者) 离哪个顶点近,就选那个顶点为公共顶点。再依次求出以公共顶点周围的4个 Cell 即可。
假设入参给定的 Level 大,即 Cell 的面积小,那么也需要判断入参 Cell 的共顶点是位于当前 Cell (函数调用者)的4个顶点的哪个顶点上。Cell 是一个矩形,有4个顶点。入参 Cell 离哪个顶点近,就选那个顶点为公共顶点。再依次求出以公共顶点周围的4个 Cell 即可。
由于需要判断位于一个 Cell 的四等分的哪一个,所以需要判断它的4个孩子的位置情况。即判断 Level - 1 的孩子的相对位置情况。
halfSize := sizeIJ(level + 1)
size := halfSize << 1
f, i, j, _ := ci.faceIJOrientation()
var isame, jsame bool
var ioffset, joffset int
这里需要拿到 halfSize ,halfSize 其实就是入参 Cell 的孩子的格子的 size 。
if i&halfSize != 0 {
// 位于后边一列,所以偏移量要加上一个格子
ioffset = size
isame = (i + size) < maxSize
} else {
// 位于左边一列,所以偏移量要减去一个格子
ioffset = -size
isame = (i - size) >= 0
}
这里我们根据 halfSize 那一位是否为1来判断距离矩形的4个顶点哪个顶点近。这里还需要注意的是,如果 i + size 不能超过 maxSize,如果超过了,就不在同一个 face 上了。同理, i - size 也不能小于 0,小于0页不在同一个 face 上了。
j 轴判断原理和 i 完全一致。
if j&halfSize != 0 {
// 位于上边一行,所以偏移量要加上一个格子
joffset = size
jsame = (j + size) < maxSize
} else {
// 位于下边一行,所以偏移量要减去一个格子
joffset = -size
jsame = (j - size) >= 0
}
最后计算结果,先把入参的 Cell 先计算出来,然后在把它周围2个轴上的 Cell 计算出来。
results := []CellID{
ci.Parent(level),
cellIDFromFaceIJSame(f, i+ioffset, j, isame).Parent(level),
cellIDFromFaceIJSame(f, i, j+joffset, jsame).Parent(level),
}
如果 i,j 都在同一个 face 上,那么共顶点就肯定不是位于外切立方体的8个顶点上了。那么就可以再把第四个共顶点的 Cell 计算出来。
if isame || jsame {
results = append(results, cellIDFromFaceIJSame(f, i+ioffset, j+joffset, isame && jsame).Parent(level))
}
综上,完整的计算共顶点邻居的代码实现如下:
func (ci CellID) VertexNeighbors(level int) []CellID {
halfSize := sizeIJ(level + 1)
size := halfSize << 1
f, i, j, _ := ci.faceIJOrientation()
fmt.Printf("halfsize 原始的值 = %v-%b\n", halfSize, halfSize)
var isame, jsame bool
var ioffset, joffset int
if i&halfSize != 0 {
// 位于后边一列,所以偏移量要加上一个格子
ioffset = size
isame = (i + size) < maxSize
} else {
// 位于左边一列,所以偏移量要减去一个格子
ioffset = -size
isame = (i - size) >= 0
}
if j&halfSize != 0 {
// 位于上边一行,所以偏移量要加上一个格子
joffset = size
jsame = (j + size) < maxSize
} else {
// 位于下边一行,所以偏移量要减去一个格子
joffset = -size
jsame = (j - size) >= 0
}
results := []CellID{
ci.Parent(level),
cellIDFromFaceIJSame(f, i+ioffset, j, isame).Parent(level),
cellIDFromFaceIJSame(f, i, j+joffset, jsame).Parent(level),
}
if isame || jsame {
results = append(results, cellIDFromFaceIJSame(f, i+ioffset, j+joffset, isame && jsame).Parent(level))
}
return results
}
下面来举几个例子。
第一个例子是相同大小 Cell 。入参和调用者 Cell 都是相同 Level - 10 的。
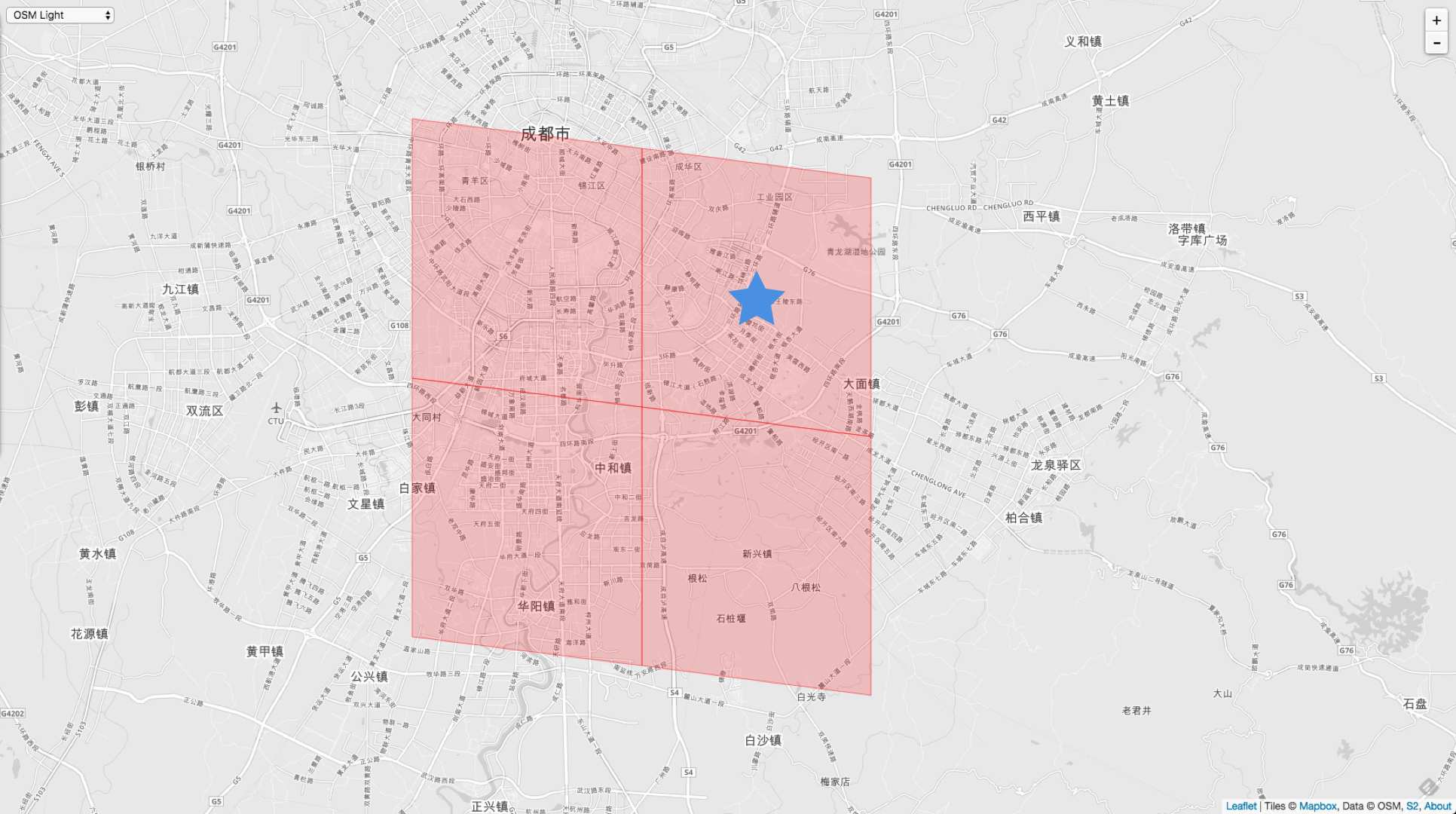
VertexNeighbors := cellID.Parent(10).VertexNeighbors(10)
// 11011011101111110011110000000000000000000000000000000000000000
3958610196388904960 // 右上角
3958599201272627200 // 左上角
3958603599319138304 // 右下角
3958601400295882752 // 左下角
第二个例子是不是大小的 Cell 。调用者 Cell 是默认 Level - 30 的。
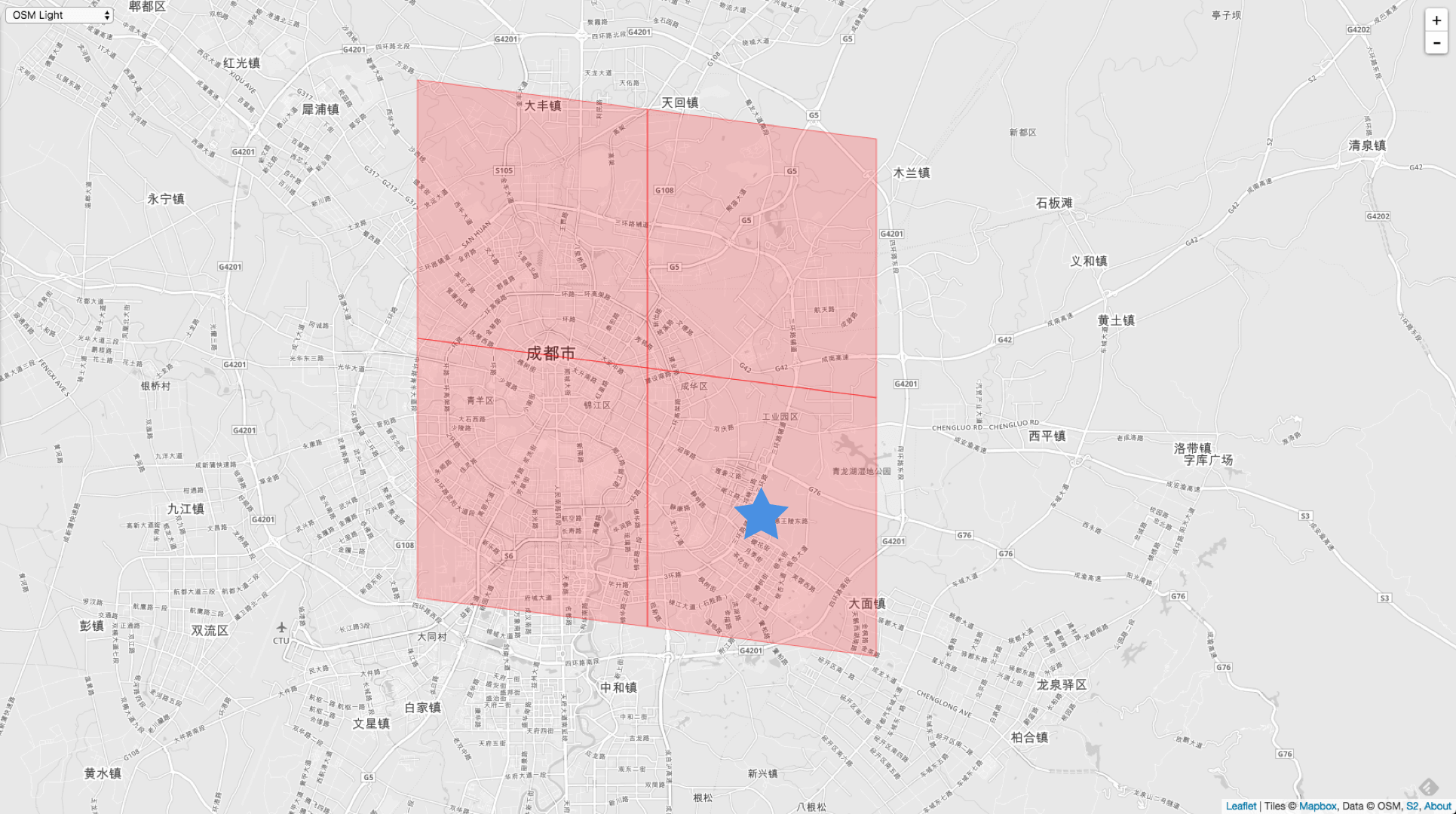
VertexNeighbors := cellID.VertexNeighbors(10)
// 11011011101111110011110000000000000000000000000000000000000000
3958610196388904960 // 右下角
3958599201272627200 // 左下角
3958612395412160512 // 右上角
3958623390528438272 // 左上角
上面两个例子可以说明一个问题,同样是调用 VertexNeighbors(10) 得到的 Cell 都是 Level - 10 的,但是方向和位置是不同的。本质在它们共的顶点是不同的,所以生成出来的4个Cell生成方向也就不同。
在 C++ 的版本中,查找顶点邻居有一个限制:
DCHECK_LT(level, this->level());
入参的 Level 必须严格的比要找的 Cell 的 Level 小才行。也就是说入参的 Cell 的格子面积大小要比 Cell 格子大小更小才行。但是在 Go 的版本实现中并没有这个要求,入参或大或小都可以。
下面这个举例,入参比 Cell 的 Level 小。(可以看到成都市已经小成一个点了)
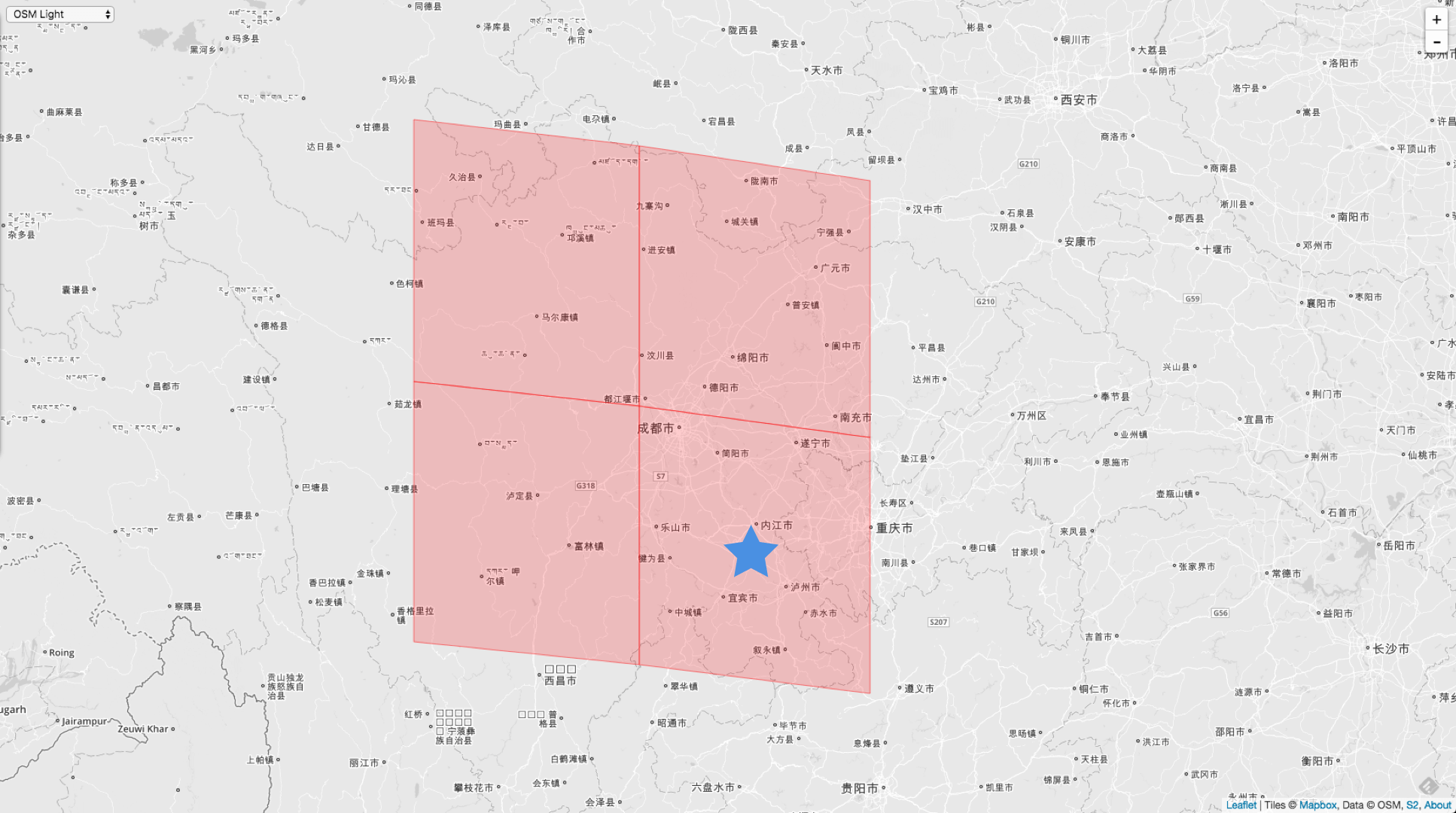
VertexNeighbors := cellID.Parent(10).VertexNeighbors(5)
3957538172551823360 // 右下角
3955286372738138112 // 左下角
3959789972365508608 // 右上角
3962041772179193856 // 左上角
下面这个举例,入参比 Cell 的 Level 大。(可以看到 Level 15 的面积已经很小了)
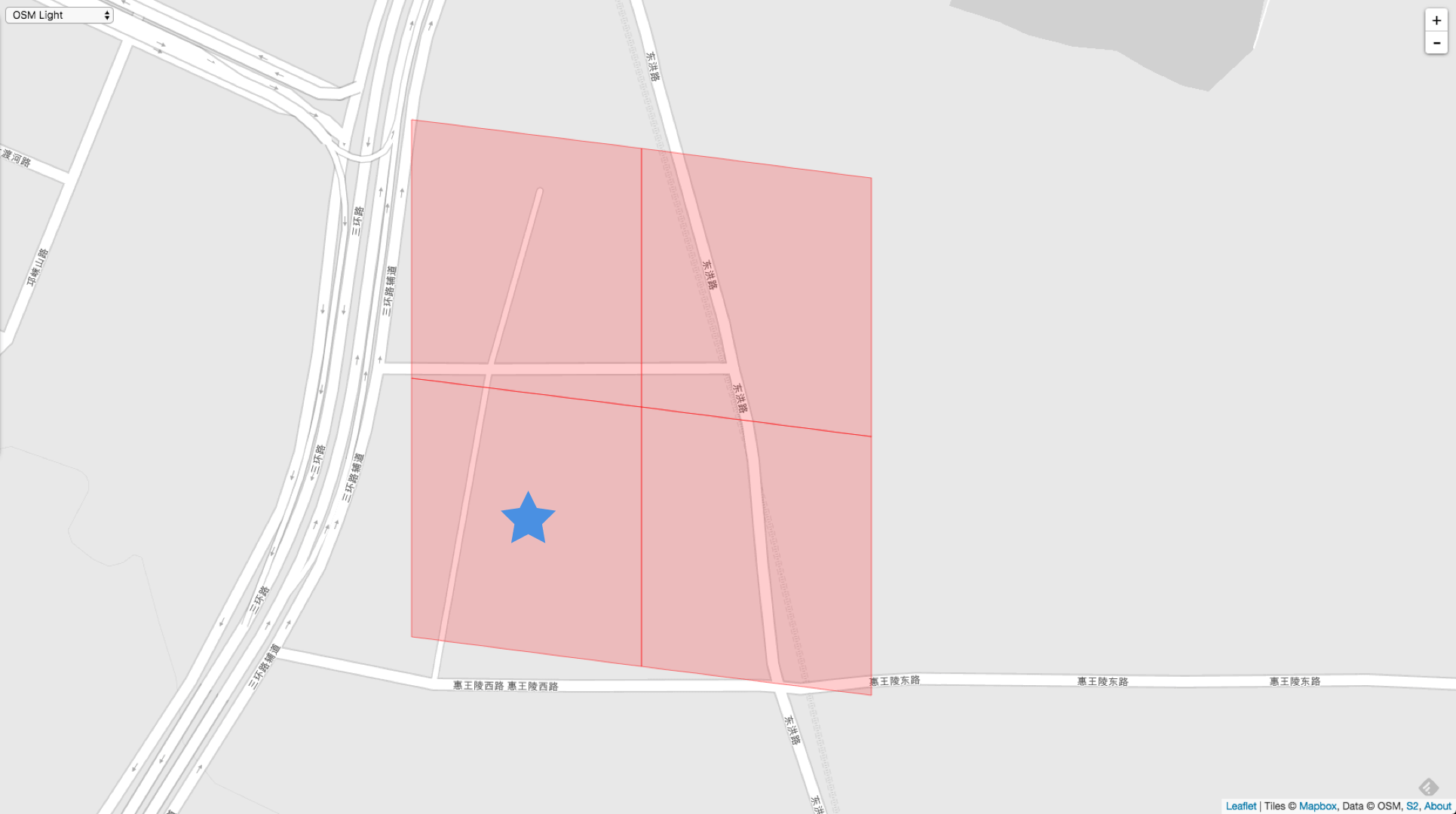
VertexNeighbors := cellID.Parent(10).VertexNeighbors(15)
3958610197462646784 // 左下角
3958610195315163136 // 右下角
3958610929754570752 // 左上角
3958609463023239168 // 右上角
三. 全邻居
最后回来文章开头问的那个问题中。如何在四叉树上如何求希尔伯特曲线的邻居 ?经过前文的一些铺垫,再来看这个问题,也许读者心里已经明白该怎么做了。
查找全邻居有一个要求,就是入参的 Level 的面积必须要比调用者 Cell 的小或者相等。即入参 Level 值不能比调用者的 Level 小。因为一旦小了以后,邻居的 Cell 的面积变得巨大,很可能一个邻居的 Cell 里面就装满了原来 Cell 的所有邻居,那这样的查找并没有任何意义。
举个例子,如果入参的 Level 比调用者 Cell 的 Level 小。那么查找它的全邻居的时候,查出来会出现如下的情况:
AllNeighbors := cellID.Parent(10).AllNeighbors(5)
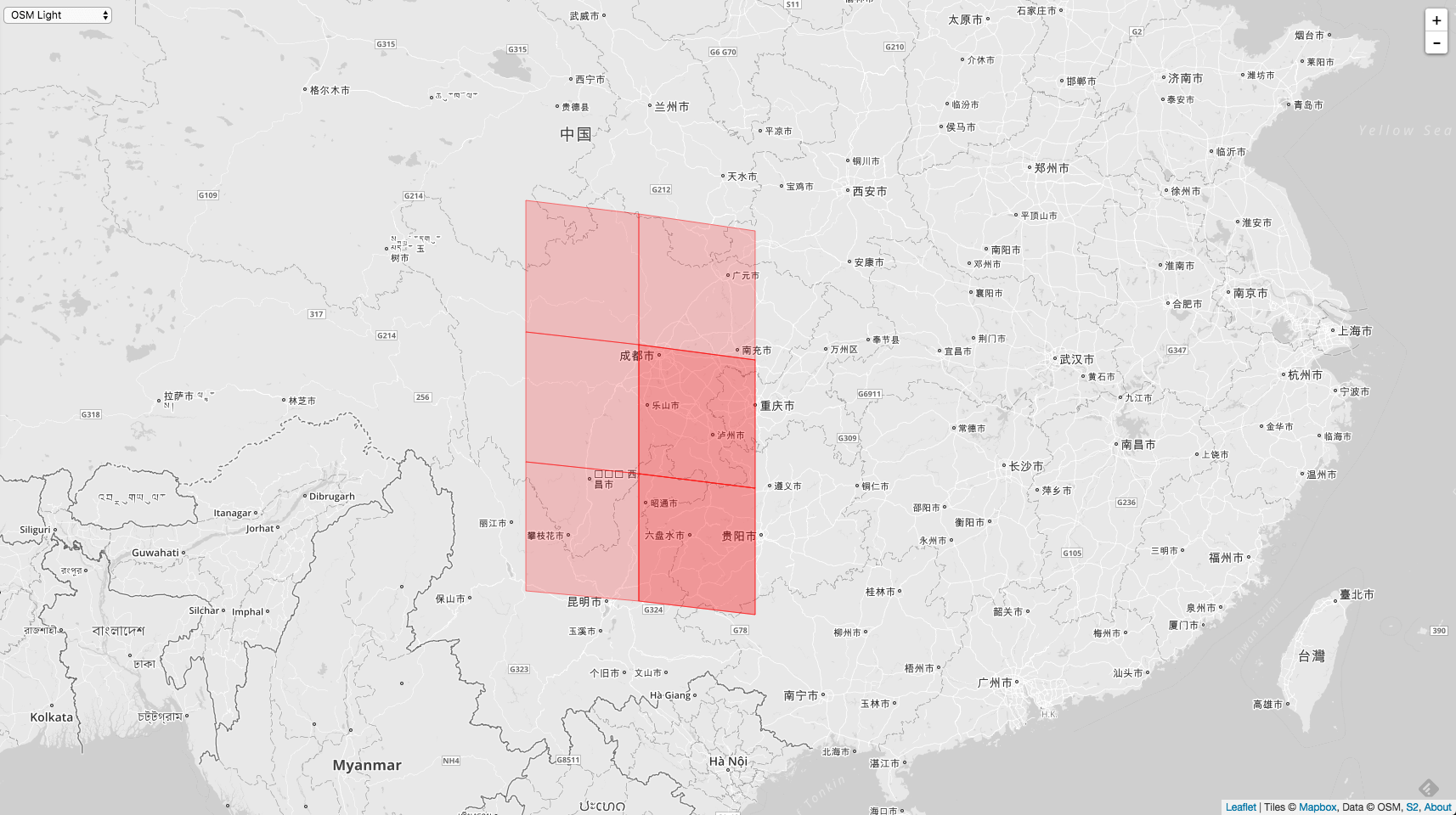
这个时候是可以查找到全邻居的,但是可能会出现重叠 Cell 的情况,为何会出现这样的现象,下面再分析。
如果入参和调用者 Cell 的 Level 是相同的,那么查找到的全邻居就是文章开头说到的问题了。理想状态如下:
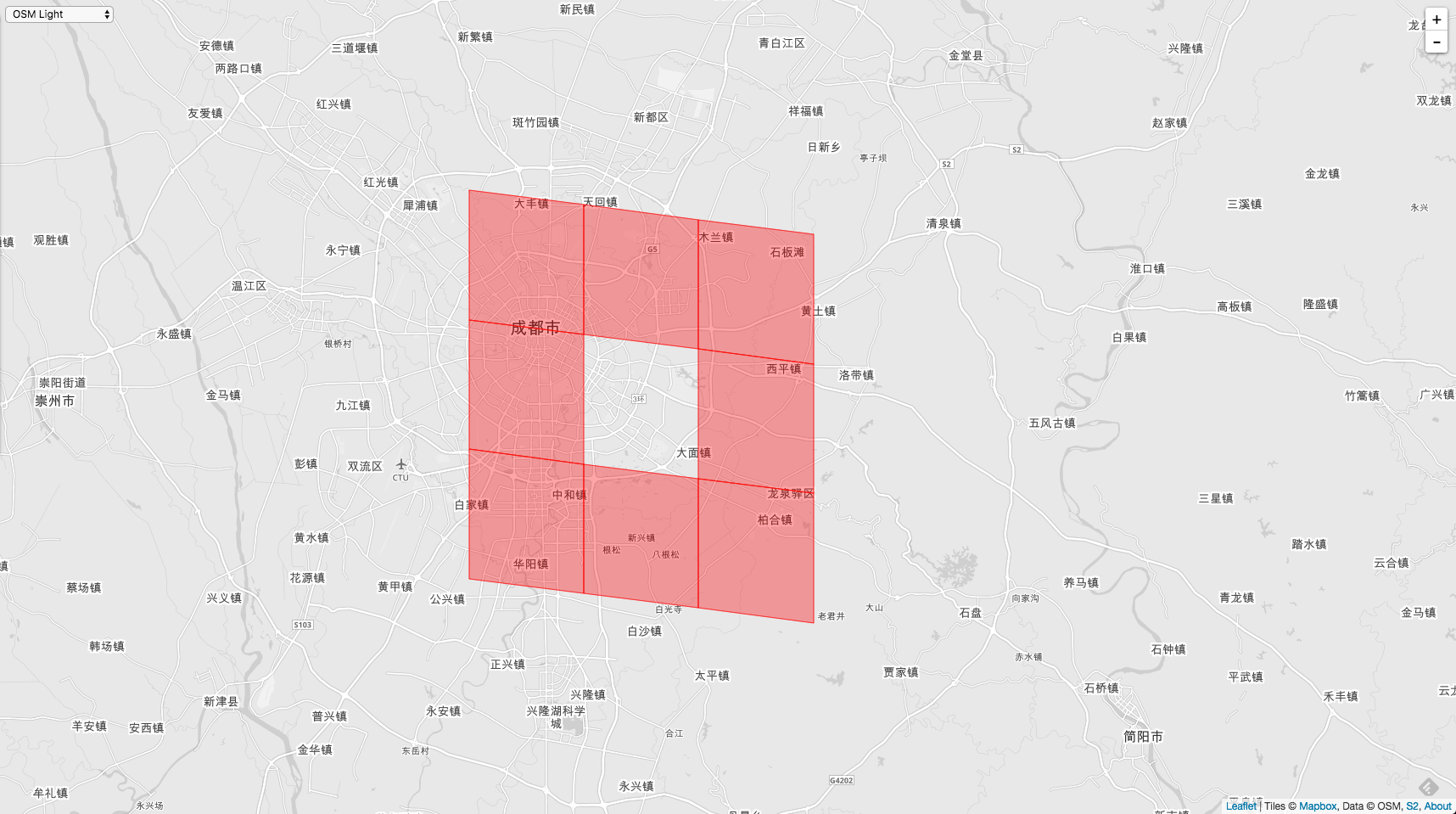
具体实现如下:
func (ci CellID) AllNeighbors(level int) []CellID {
var neighbors []CellID
face, i, j, _ := ci.faceIJOrientation()
// 寻找最左下角的叶子节点的坐标。我们需要规范 i,j 的坐标。因为入参 Level 有可能比调用者 Cell 的 Level 要大。
size := sizeIJ(ci.Level())
i &= -size
j &= -size
nbrSize := sizeIJ(level)
for k := -nbrSize; ; k += nbrSize {
var sameFace bool
if k < 0 {
sameFace = (j+k >= 0)
} else if k >= size {
sameFace = (j+k < maxSize)
} else {
sameFace = true
// 上边邻居 和 下边邻居
neighbors = append(neighbors, cellIDFromFaceIJSame(face, i+k, j-nbrSize,
j-size >= 0).Parent(level))
neighbors = append(neighbors, cellIDFromFaceIJSame(face, i+k, j+size,
j+size < maxSize).Parent(level))
}
// 左边邻居,右边邻居,以及2个对角线上的顶点邻居
neighbors = append(neighbors, cellIDFromFaceIJSame(face, i-nbrSize, j+k,
sameFace && i-size >= 0).Parent(level))
neighbors = append(neighbors, cellIDFromFaceIJSame(face, i+size, j+k,
sameFace && i+size < maxSize).Parent(level))
// 这里的判断条件有2个用途,一是防止32-bit溢出,二是循环的退出条件,大于size以后也就不用再找了
if k >= size {
break
}
}
return neighbors
}
上述代码简单的思路用注释写了。需要讲解的部分现在来讲解。
首先需要理解的是 nbrSize 和 size 的关系。为何会有 nbrSize ? 因为入参 Level 是可以和调用者 Cell 的 Level 不一样的。入参的 Level 代表的 Cell 可大可小也可能相等。最终结果是以 nbrSize 格子大小来表示的,所以循环中需要用 nbrSize 来控制格子的大小。而 size 只是原来调用者 Cell 的格子大小。
循环中 k 的变化,当 k = -nbrSize 的时候,这个时候循环只会计算左边和右边的邻居。对角线上的顶点邻居其实也是左边邻居和右边邻居的一种特殊情况。接下来 k = 0,就会开始计算上边邻居和下边邻居了。k 不断增加,直到最后 k >= size ,最后一次循环内,会先计算一次左边和右边邻居,再 break 退出。
调用者的 Cell 在中间位置,所以想要跳过这个 Cell 到达另外一边(上下,或者左右),那么就需要跳过 size 的大小。具体代码实现是 i + size 和 j + size 。
先看左右邻居的循环扫描方式。
左邻居是 i - nbrSize,j + k,k 在循环。这表示的就是左邻居的生成方式。它生成了左邻居一列。从左下角开始生成,一直往上生成到左上角。
右邻居是 i + size,j + k,k 在循环。这表示的就是右邻居的生成方式。它生成了右邻居一列。从右下角开始生成,一直往上生成到右上角。
再看上下邻居的循环扫描方式。
下邻居是 i + k,j - nbrSize,k 在循环。这表示的就是下邻居的生成方式。它生成了下邻居一行。从下邻居最左边开始生成,一直往上生成到下邻居最右边。
上邻居是 i + k,j + size,k 在循环。这表示的就是上邻居的生成方式。它生成了上邻居一行。从上邻居最左边开始生成,一直往上生成到上邻居最右边。
举例:
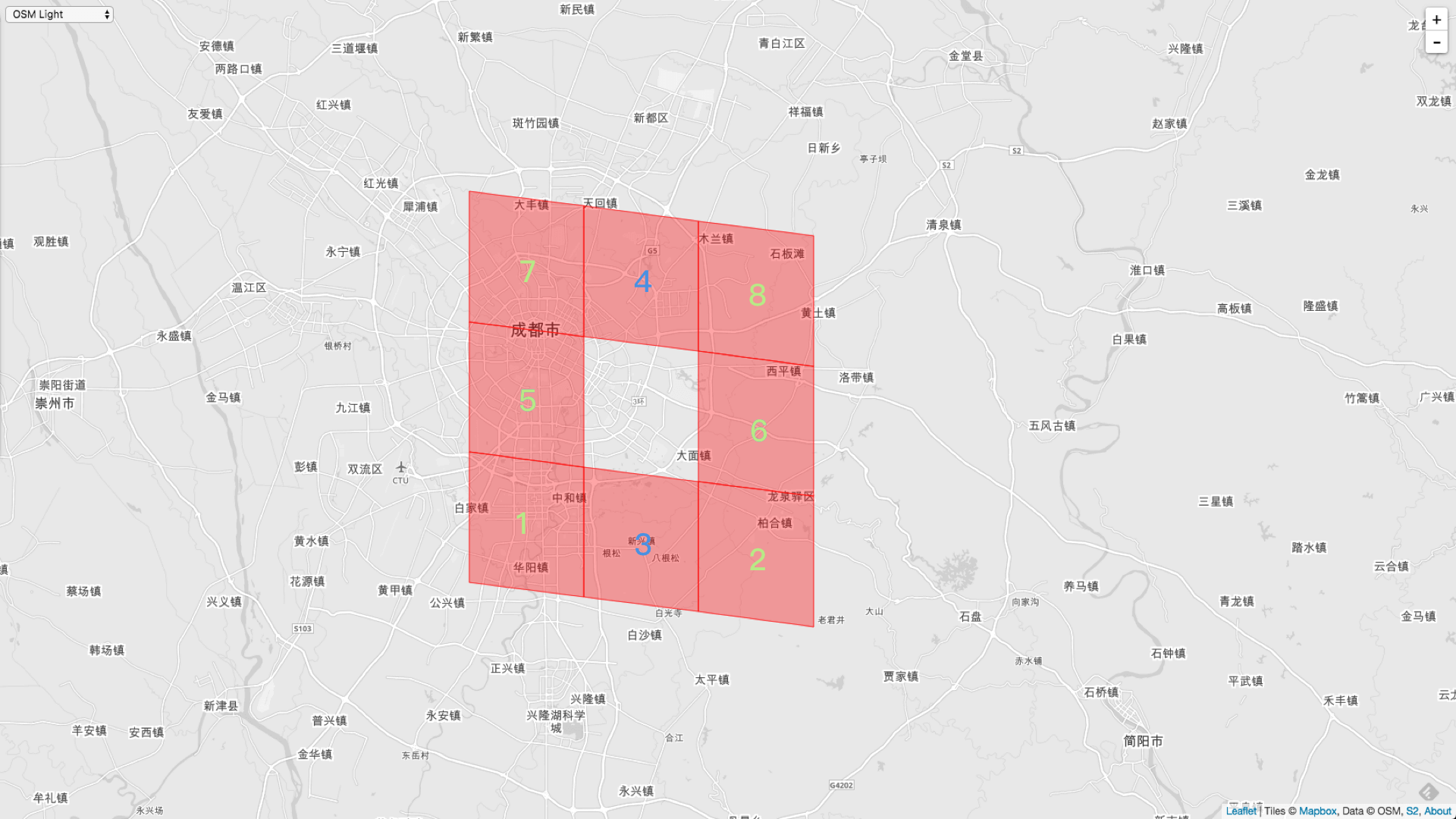
中间 Cell 的周围的全邻居是上图的 8 的相同 Level 的 Cell。
生成顺序用需要标识出来了。1,2,5,6,7,8 都是左右邻居生成出来的。3,4 是上下邻居生成出来的。
上面这个例子是都是 Level - 10 的 Cell 生成出来的。全邻居正好是8个。
AllNeighbors := cellID.Parent(10).AllNeighbors(10)
3958601400295882752,
3958605798342393856,
3958603599319138304,
3958612395412160512,
3958599201272627200,
3958607997365649408,
3958623390528438272,
3958614594435416064
再举一个 Level 比调用者 Cell 的 Level 大的例子。
AllNeighbors := cellID.Parent(10).AllNeighbors(11)
3958600575662161920,
3958606622976114688,
3958603324441231360,
3958611570778439680,
3958600025906348032,
3958607172731928576,
3958603874197045248,
3958613220045881344,
3958599476150534144,
3958608821999370240,
3958623115650531328,
3958613769801695232
它的全邻居生成顺序如下:
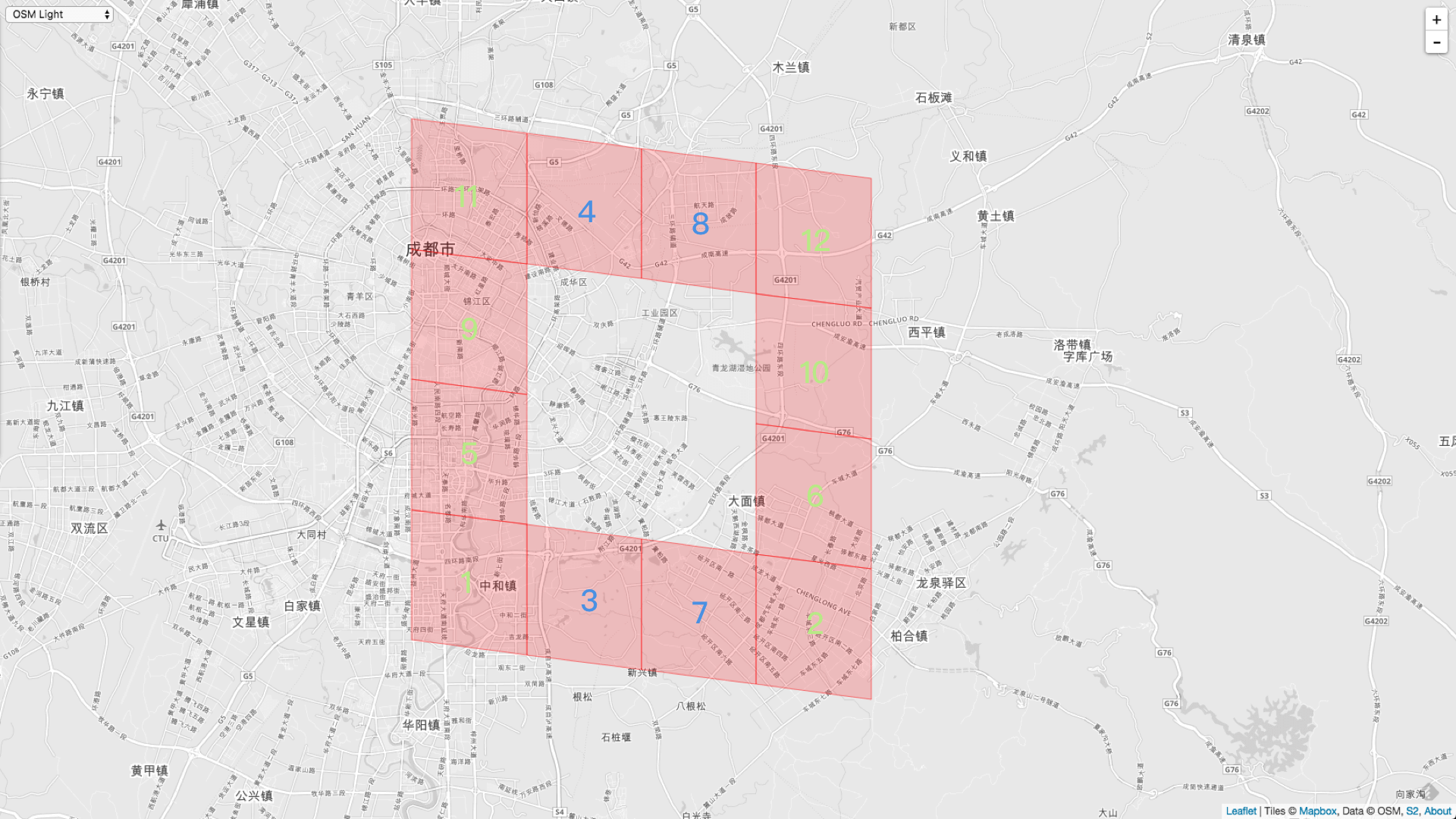
1,2,5,6,9,10,11,12 都是左右邻居,3,4,7,8 是上下邻居。我们可以看到左右邻居是从下往上生成的。上下邻居是从左往右生成的。
如果 Level 更大,比如 Level - 15 ,就会生成更多的邻居:
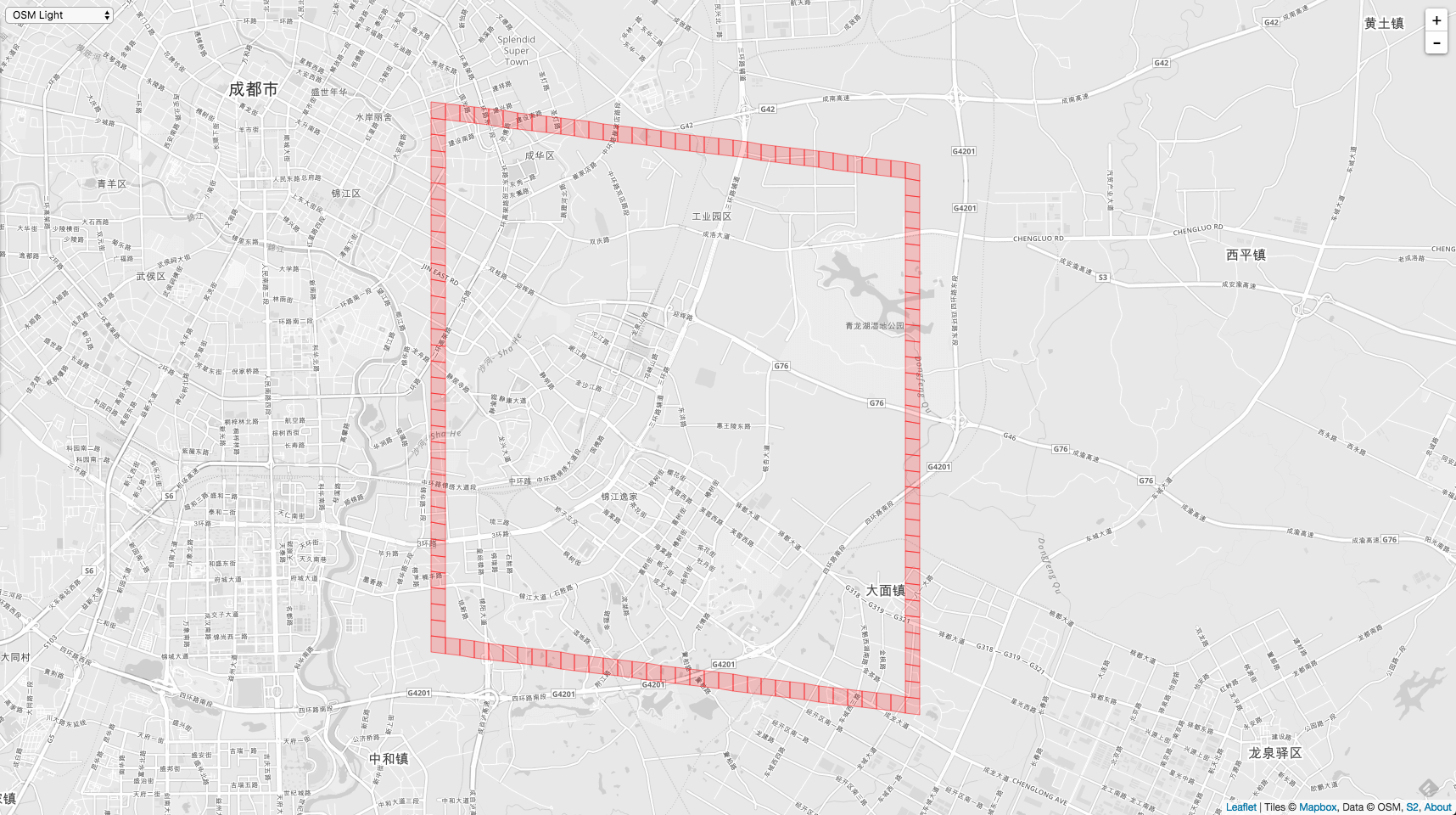
现在在解释一下如果入参 Level 比调用者 Cell 的 Level 小的情况。
举例,入参 Level = 9 。
AllNeighbors := cellID.Parent(10).AllNeighbors(9)
3958589305667977216,
3958580509574955008,
3958580509574955008,
3958615693947043840,
3958598101760999424,
3958606897854021632,
3958624490040066048,
3958615693947043840
生成的全邻居如下:
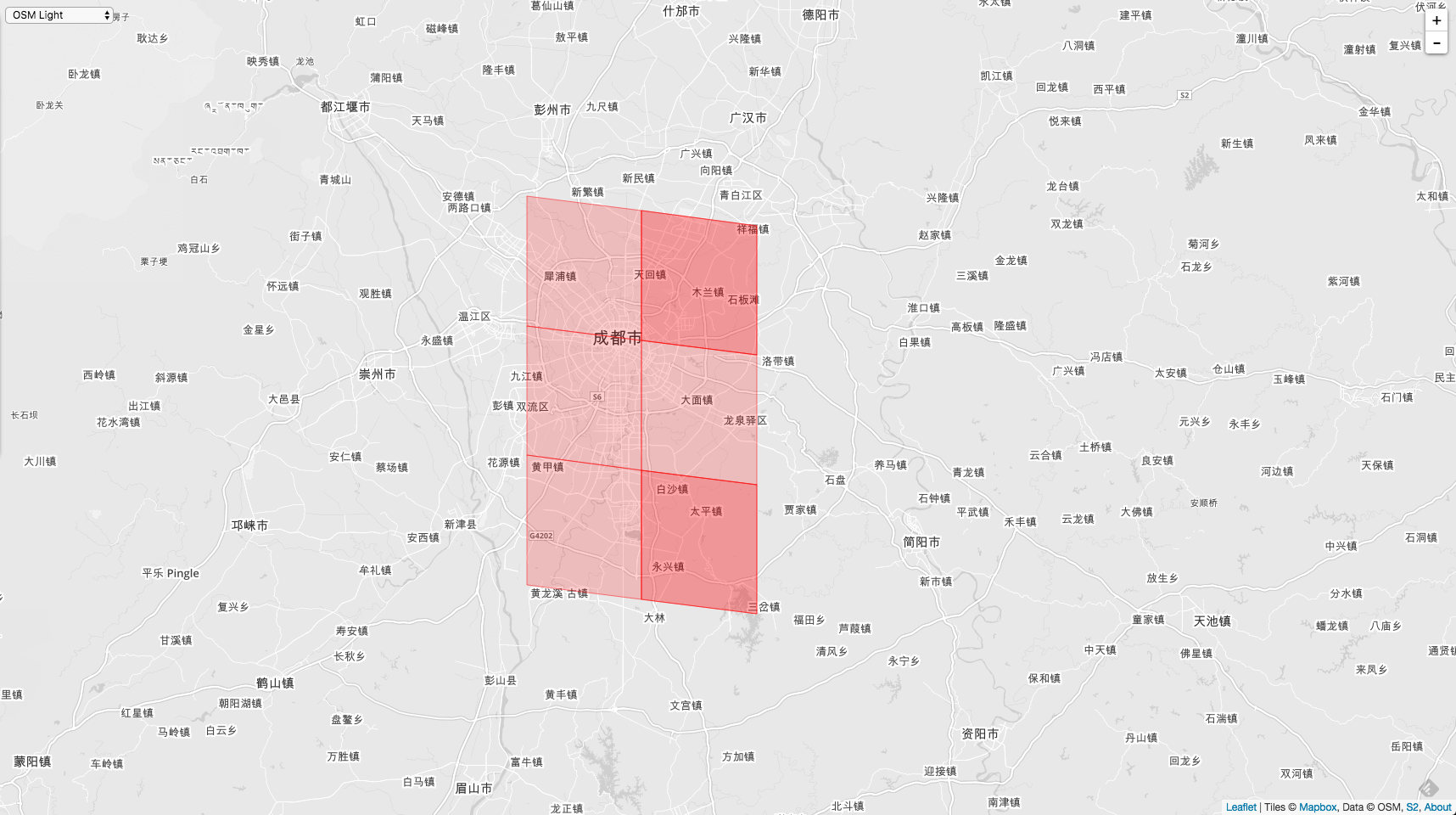
可以看到本来有8个邻居的,现在只有6个了。其实生成出来的还是8个,只不过有2个重复了。重复的见图中深红色的两个 Cell。
为何会重叠?
中间调用者的 Level - 10 的 Cell 先画出来。
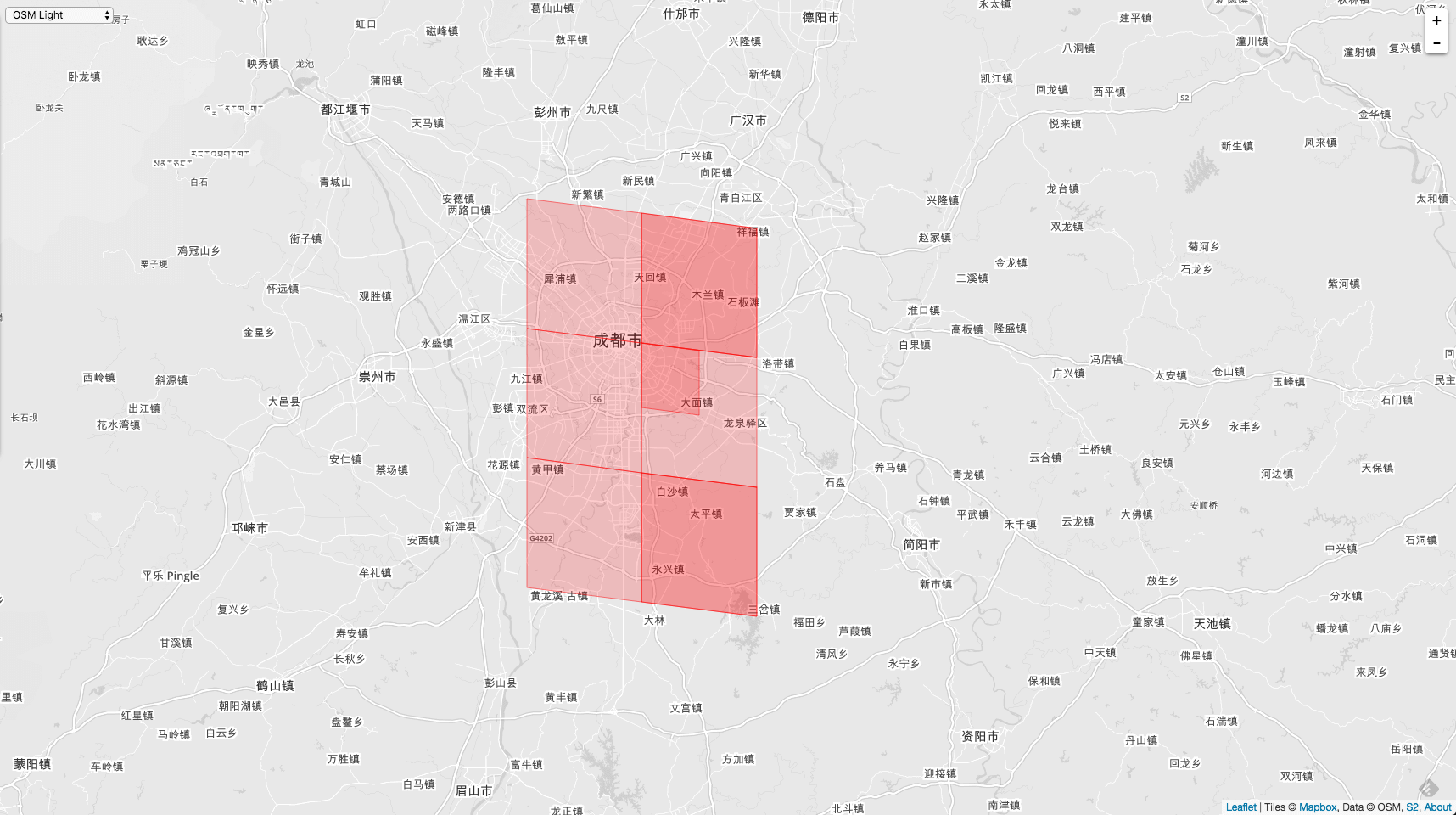
因为是 Level - 9 的,所以它是中间那个 Cell 的四分之一。
我们把 Level - 10 的两个上邻居也画出来。
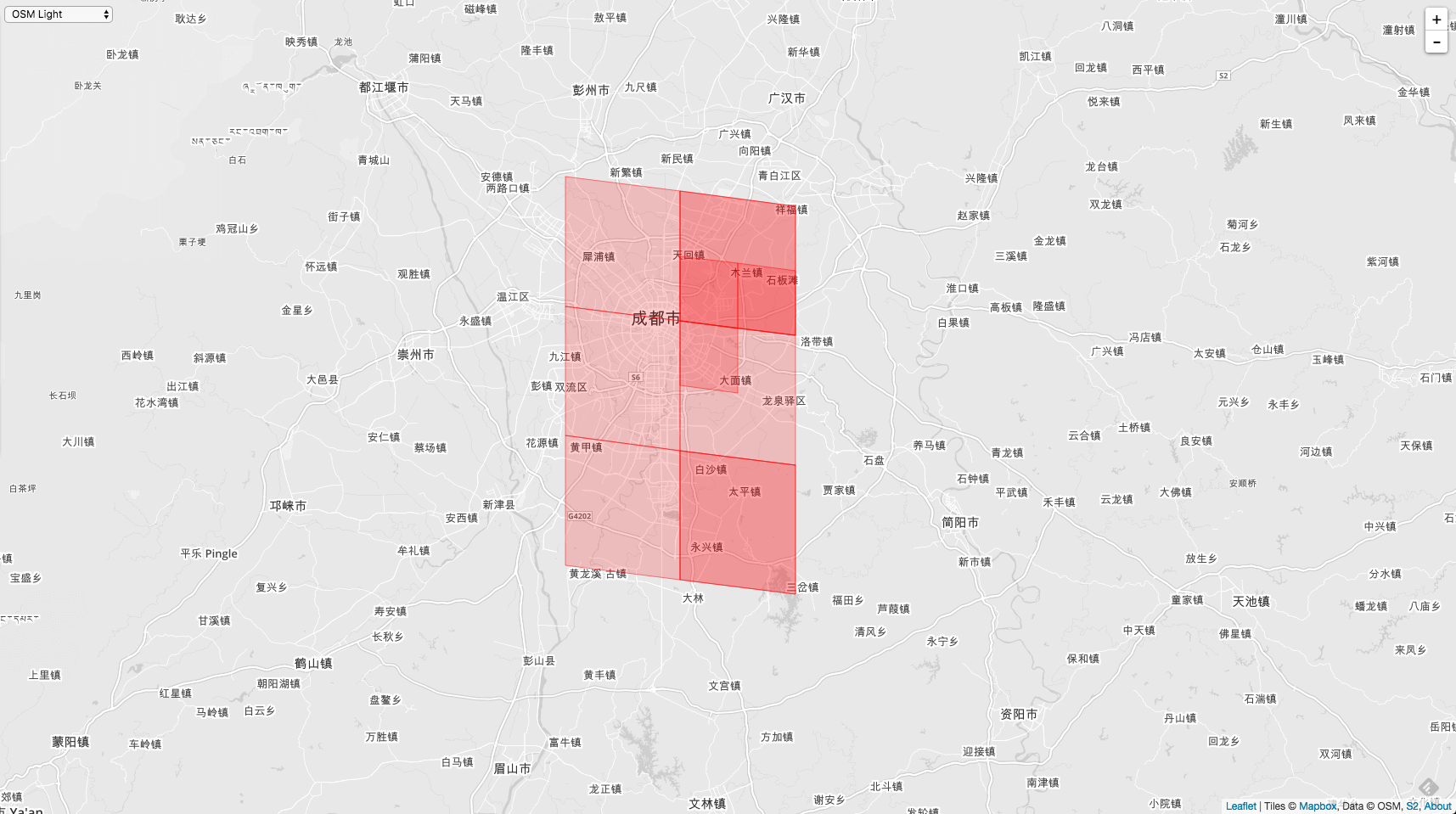
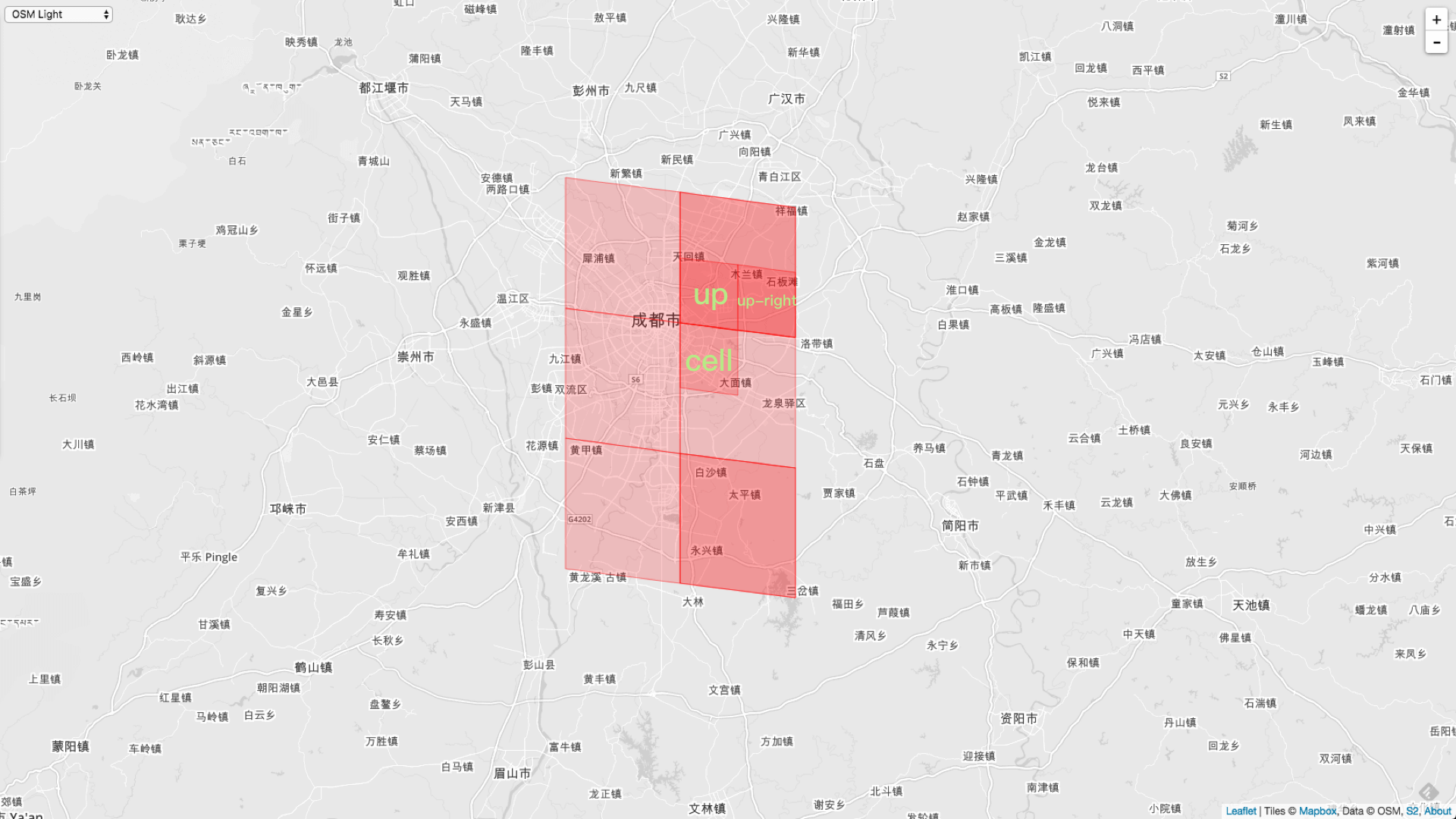
可以看到上邻居 Up 和顶点邻居 up-right 都位于同一个 Level - 9 的 Cell 内了。所以上邻居和右上角的顶点邻居就都是同一个 Level - 9 的 Cell 。所以重叠了。同理,下邻居和右下的顶点邻居也重叠了。所以就会出现2个 Cell 重叠的情况。
而且中间也没有空出调用者 Cell 的位置。因为 i + size 以后,范围还在同一个 Level - 9 的 Cell 内。
如果 Level 更小,重叠情况又会发生变化。比如 Level - 5 。
AllNeighbors := cellID.Parent(10).AllNeighbors(5)
3953034572924452864,
3946279173483397120,
3946279173483397120,
3957538172551823360,
3955286372738138112,
3957538172551823360,
3962041772179193856,
3959789972365508608
画在地图上就是
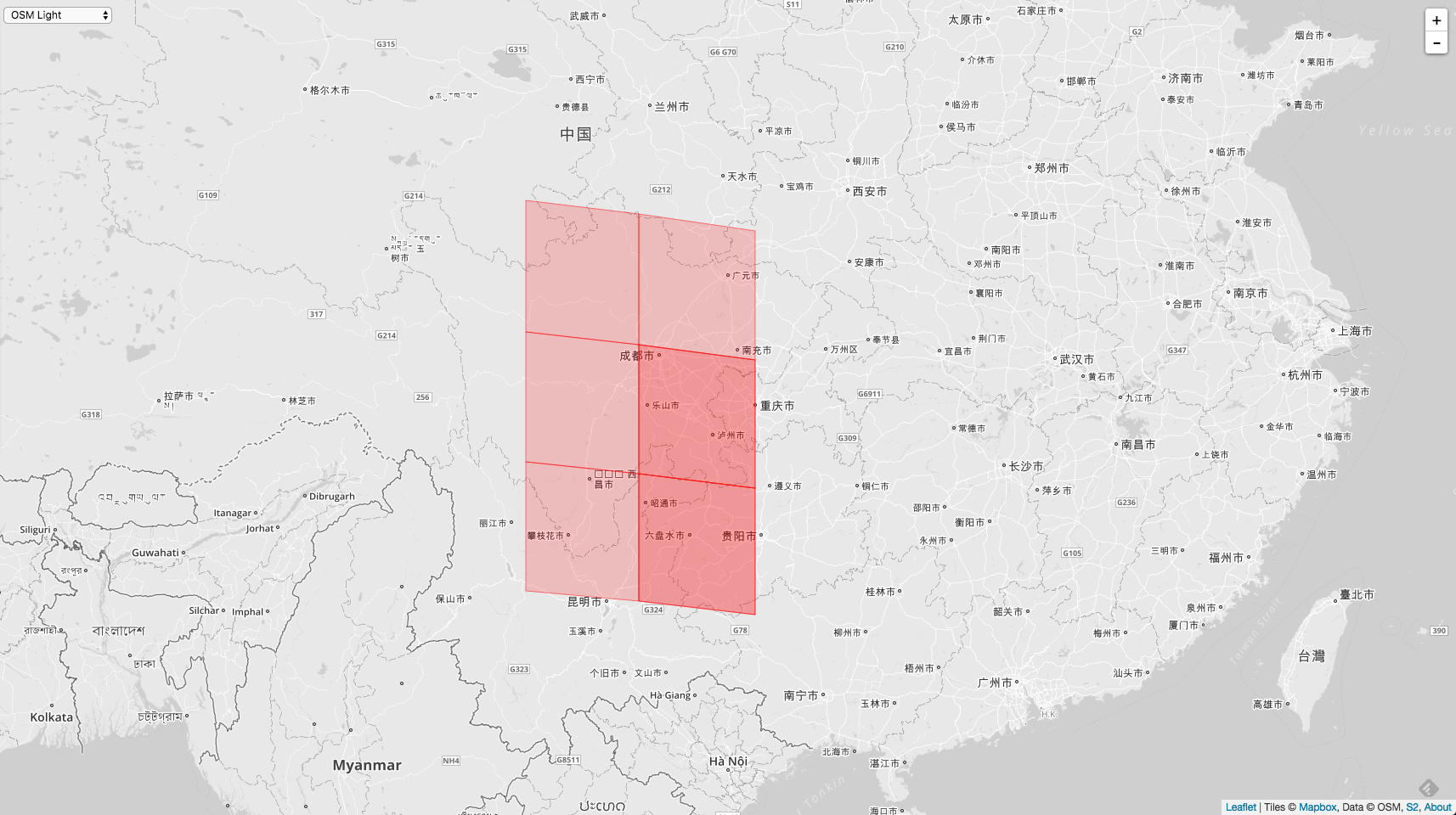
重叠的位置也发生了变化。
至此,查找邻居相关的算法都介绍完了。
空间搜索系列文章:
如何理解 n 维空间和 n 维时空
高效的多维空间点索引算法 — Geohash 和 Google S2
Google S2 中的 CellID 是如何生成的 ?
Google S2 中的四叉树求 LCA 最近公共祖先
神奇的德布鲁因序列
四叉树上如何求希尔伯特曲线的邻居 ?
GitHub Repo:Halfrost-Field
Follow: halfrost · GitHub





