一、为什么需要加密
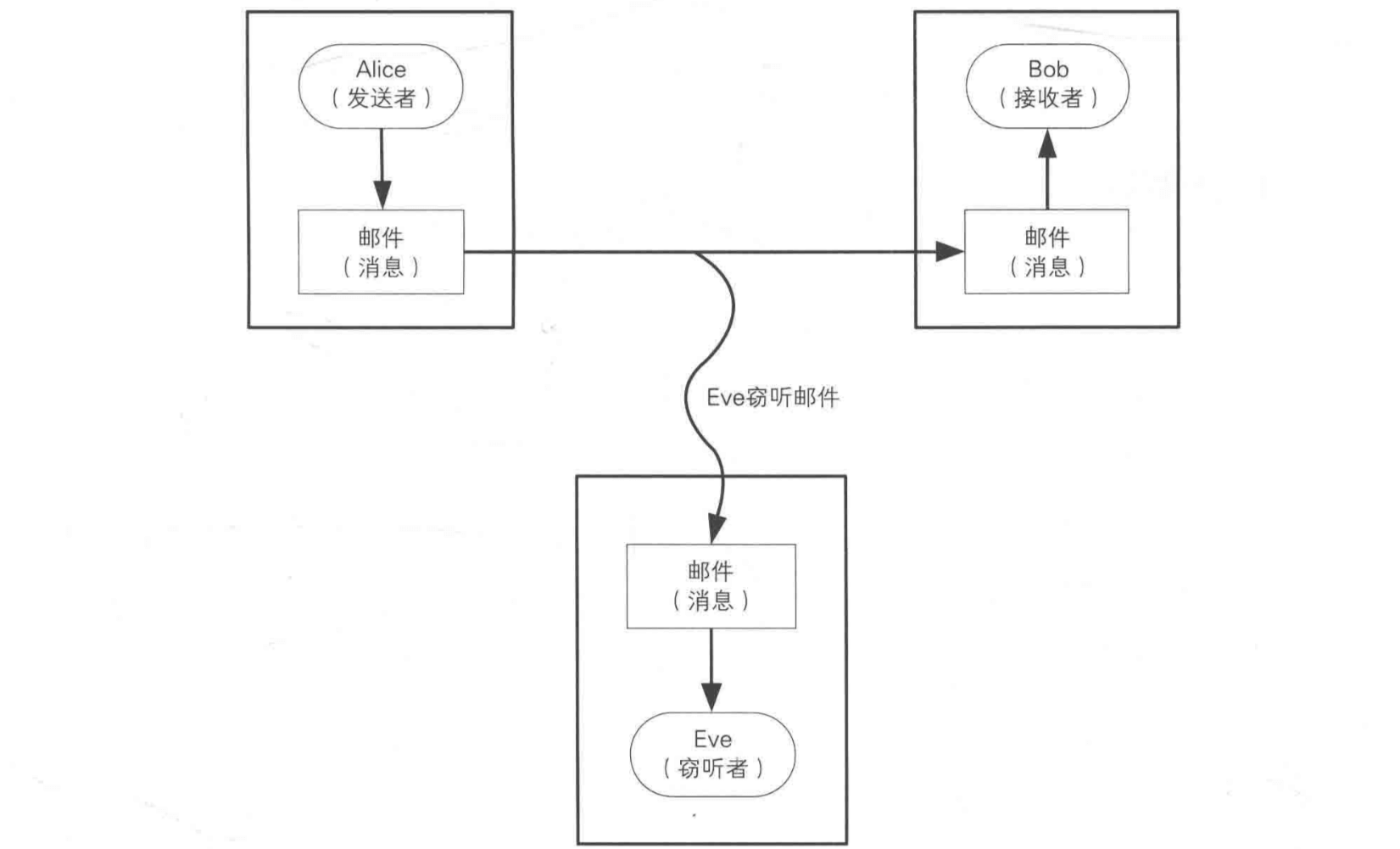
每个人都有自己的秘密,如果不加密,在网上传输很容易被监听。如果涉及到金钱相关,密码泄露以后很容易造成损失。所以都会利用加密 cryptography 技术,保证信息的机密性 confidentiality。
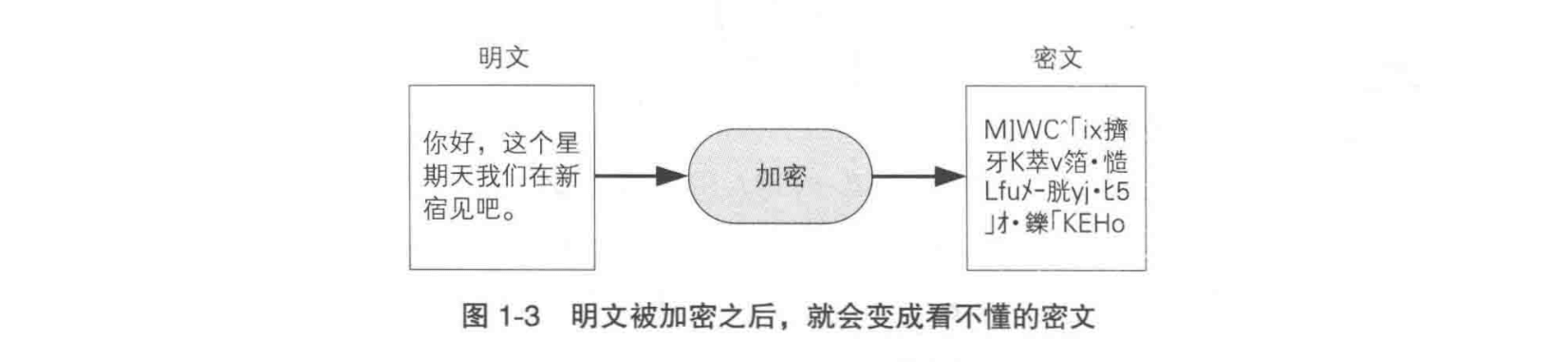
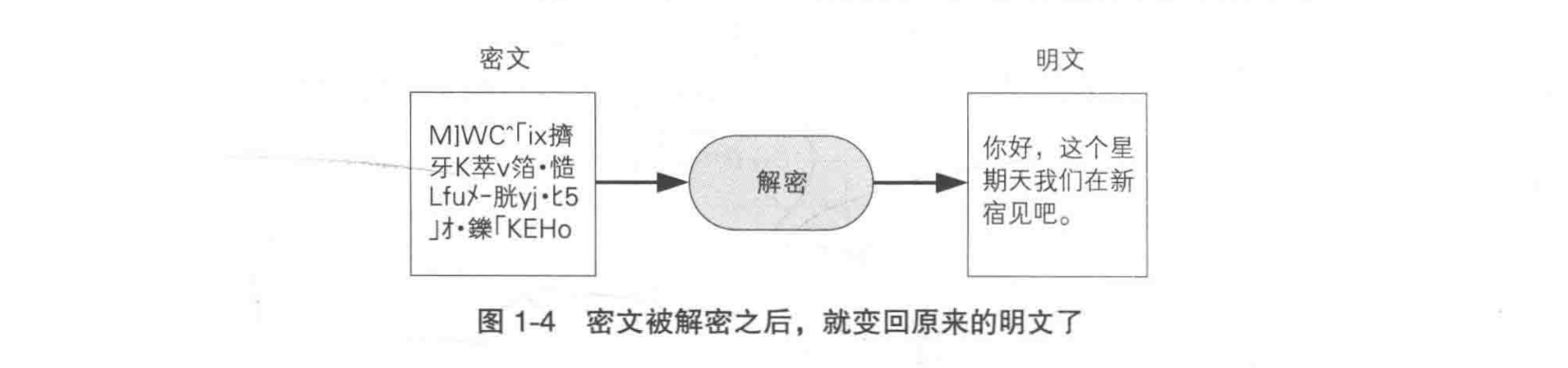
信息被加密以后变成了密文在网上传播,接收者拿到密文进行解密 cryptanalysis,解密以后就可以看到明文。
进行破译密码的人叫破译者,破译者不一定都是坏人,密码学研究者为了研究密码强度,也会需要对密码进行破译,研究者在这种情况下也是破译者。
加密与压缩的顺序?
压缩一定在加密之前。因为加密以后,比特序列的冗余性消失,基本上无法再压缩了。在加密前进行压缩的做法不仅仅限于混合密码系统,而是对所有密码都适用。
二、对称加密
对称密码 (symmetric cryptography)是指在加密和解密时使用同一密钥的方式。对应的加密方式是对称加密。目前广泛使用 AES。
对称密码有多种别名,公共密钥密码(common-key cryptography),传统密码(conventional cryptography),私钥密码(secret-key cryptography),共享密钥密码(shared-key cryptography)等。
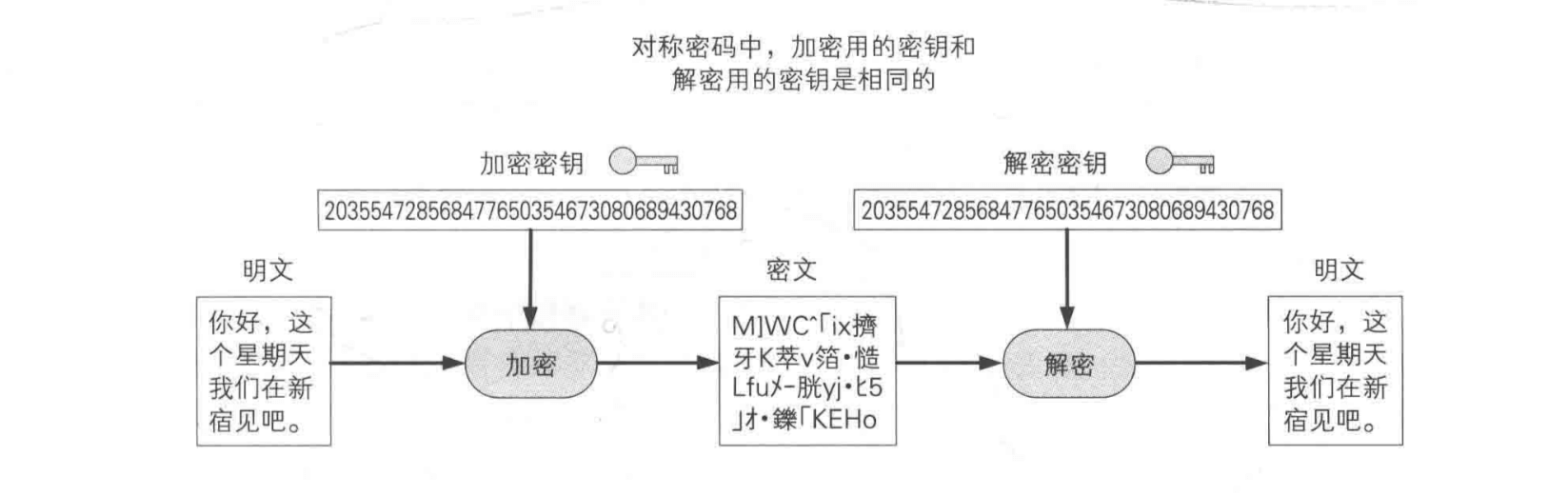
对称密码需要解决将解密密钥配送给接收者的密钥配送问题。
三、非对称加密
公钥密码 (public-key cryptography)则是指在加密和解密时使用不同密钥的方式。对应的加密方式是非对称加密。目前广泛使用 RSA。(RSA、ElGamal、Rabin、DH、ECDH)
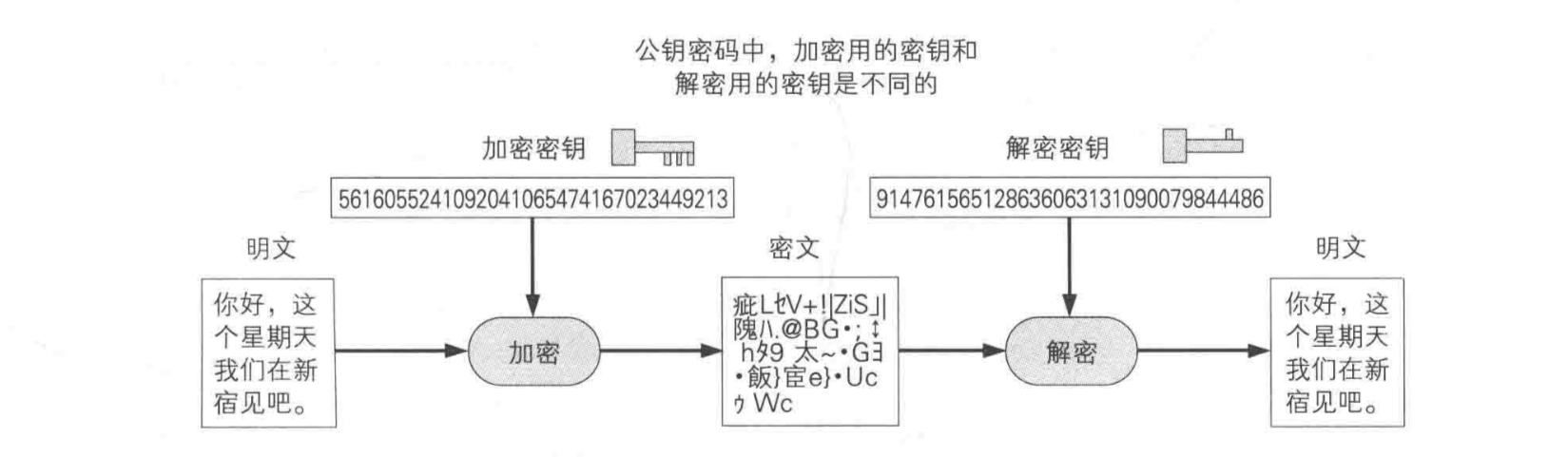
公钥密码解决了密钥配送的问题,但是存在通过中间人攻击被伪装的风险,因此需要对带有数字签名的公钥进行认证。
四、单向散列函数
网上很多免费的软件,为了防止软件被篡改,有安全意识的软件发布者会在发布软件的同时会发布这个版本软件的散列值 hash。散列值是用单向散列函数(one-way hash function)计算出来的数值。目前广泛使用 SHA-2(SHA-224、SHA-356、SHA-384、SHA-512) 和 具有全新结构的 SHA-3(Keccak 算法)
散列值 hash,又被称为哈希值,密码校验和(cryptographic checksum),指纹(fingerprint),消息摘要(message digest)。
单向散列函数并不是为了保证消息的机密性,而是完整性(integrity)。完整性指的是,数据是正确的,而不是伪造的。单向散列函数是保证信息的完整性的密码技术,它会检测数据是否被篡改。
单向散列函数可以单独使用,也可以作为消息认证码、数字签名以及伪随机数生成器等技术的组成元素使用。
五、消息认证码
为了确认消息是否来自期望的通信对象,可以通过使用消息认证码(message authentication code)。消息认证码主要是提供了认证(authentication)机制,与此同时它也能保证消息的完整性。
消息认证码中最常用的单向散列函数是 HMAC。HMAC 的构成不依赖于某一种具体的单向散列函数算法。
消息认证码能对通信对象进行认证,但无法对第三方进行认证。它也无法防止否认。消息认证码可以用来实现认证加密。
六、数字签名
试想有这样一种情况,A 欠 B 100 万美刀,于是 A 向 B 打了一张欠条。一周以后,A 拿到钱以后就不承认那张欠条是自己写的,抵赖借钱了。
这个时候就牵扯到密码学里面的防抵赖的技术 —— 数字签名。数字签名类似现实世界中的签名和盖章,数字签名是一种能防止用户抵赖,伪装,篡改和否认的密码技术。目前广泛使用的数字签名算法包括 RSA、ElGamal、DSA、椭圆曲线 DSA(ECDSA)、爱德华兹曲线 DSA(EDDSA)等。
如果用户 B 能让 A 在打欠条的时候,签上自己的签名(数字签名),这样可以防止他日后抵赖。
公钥基础设施 PKI 中使用的证书,就是对公钥加上认证机构的数字签名所构成的。要验证公钥的数字签名,需要通过某种途径获取认证机构自身的合法公钥。
七、伪随机数生成器
伪随机数生成器(Pseudo Random Number Generator,PRNG)是一种能够模拟产生随机数列的算法。伪随机数负责承担密钥生成的职责。它由密码和单向散列函数等技术构成,主要用于生成密钥、初始化向量和 nonce 等。
八、隐写术和数字水印
加密技术是为了让消息内容本身无法被读取。而隐写术是为了能够隐藏消息本身。
举个例子,比如在一个音乐里面可以隐藏一张图片,在特定的比特位上面分别插入图片的二进制位,只要记住哪些位是图片,哪些为是音乐,那么就能还原成一首音乐和一张图片。
再比如,iOS 开发中,可以把客户端本地的证书隐藏到图片资源中。这样就算怀有恶意的人拆开 ipa 安装包,咋一看也找不到证书文件,除非先逆向代码,找到隐写术的算法才能获取到证书的真实文件。
数字水印就是利用了隐写术的方法。数字水印是一种将著作权拥有者及购买者的信息嵌入文件中的技术。但是仅仅凭借数字水印技术是没有办法对信息进行保密的,所以需要结合其他的技术一起。
可以将加密和隐写术结合起来使用。类似上面证书隐藏到图片中的例子。证书是加密过的,所以证书隐藏了敏感信息,隐写术又隐藏了证书本身。
九、密码技术的实质
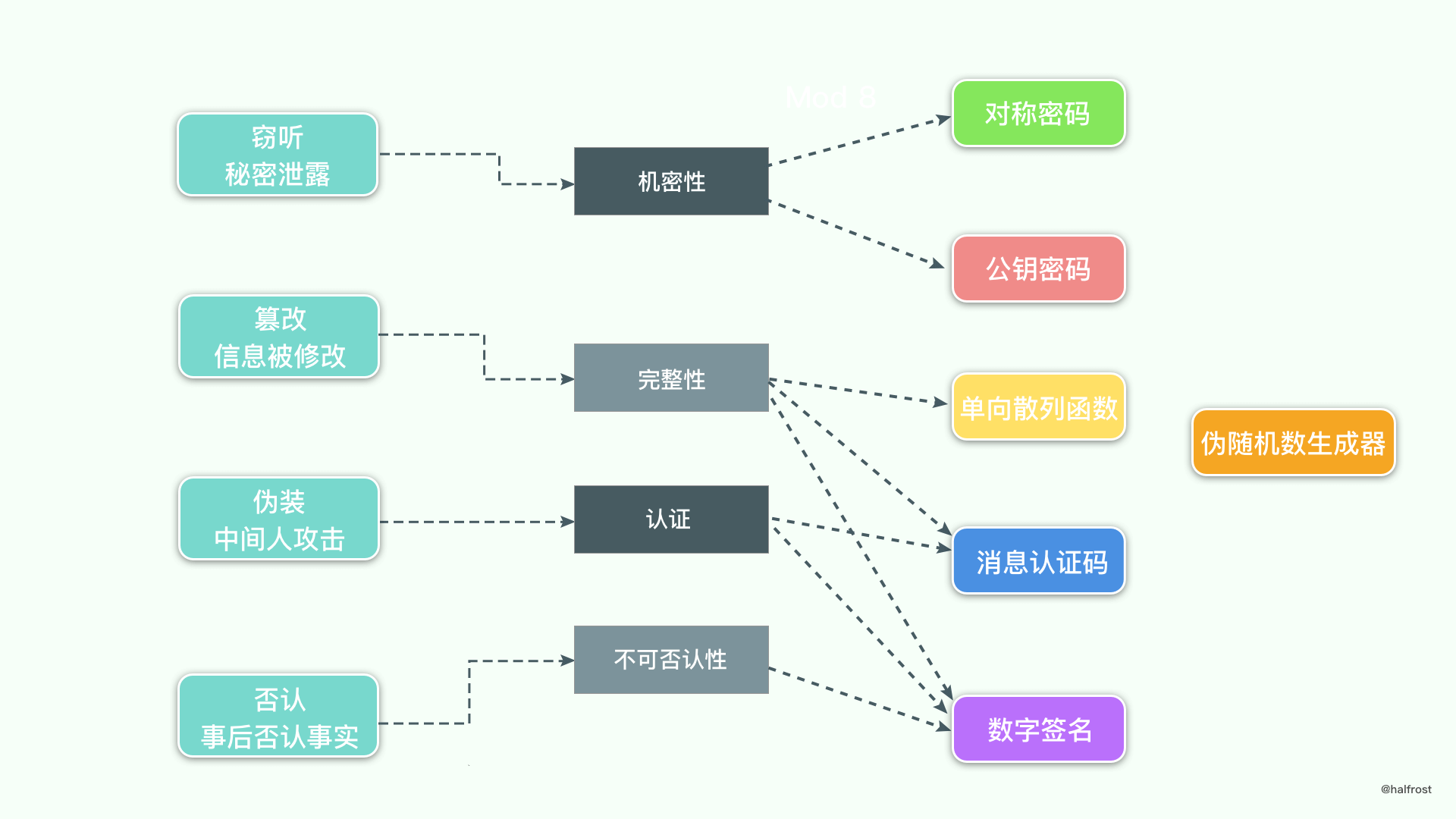
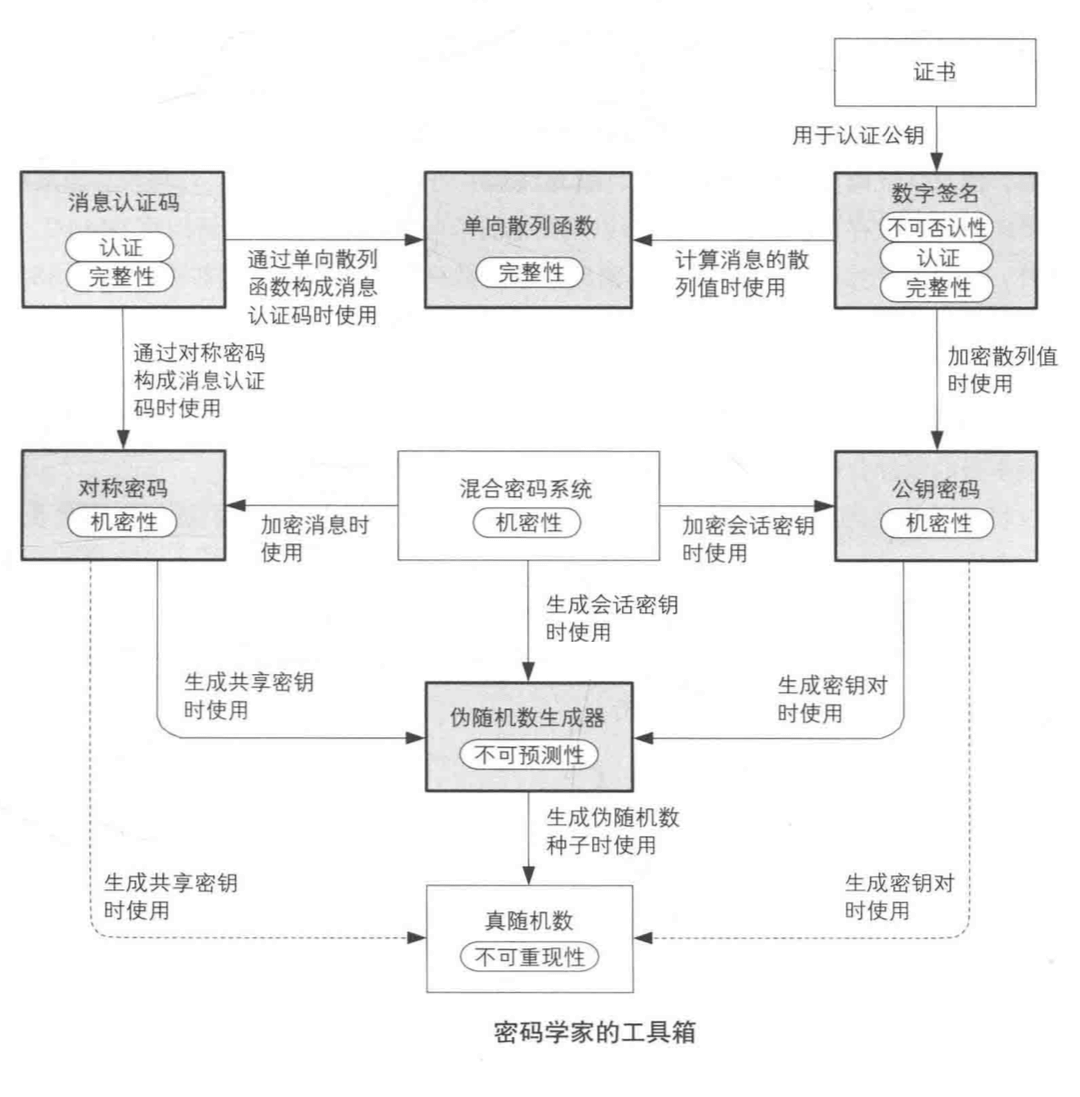
密码学家的工具箱中的内容完整整理如下:
密码技术实质是压缩技术
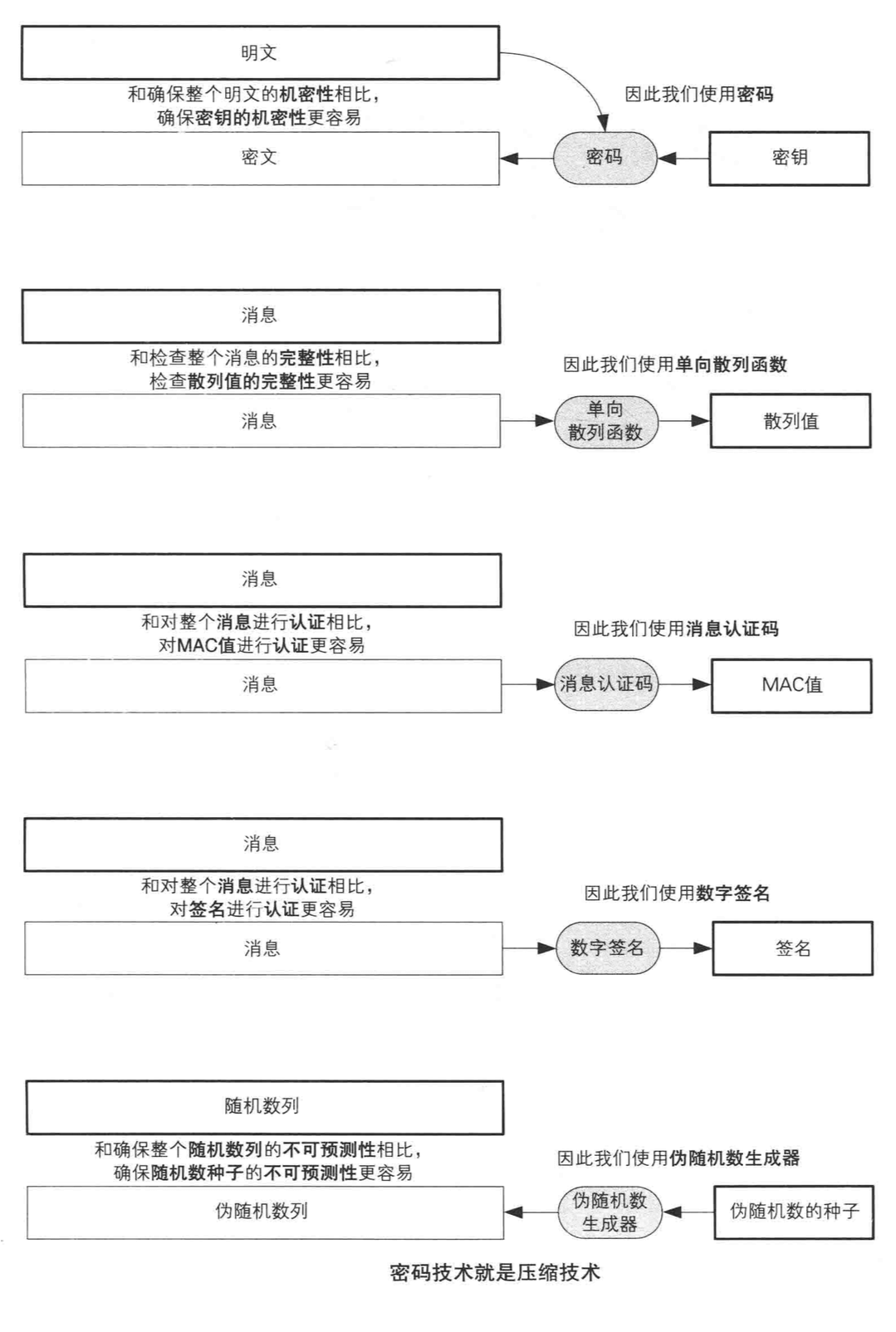
- 对称加密和公钥密码是机密性的压缩
- 单向散列函数是完整性的压缩
- 消息认证码和数字签名是认证的压缩
- 伪随机数生成器是不可预测性的压缩
在消息认证码中,MAC 值就是认证符号,在数字签名中,签名就是认证符号。两者都是通过较短的认证符号来对较长的消息进行认证。
- 密钥是机密性的精华
- 散列值是完成性的精华
- 认证符号(MAC 值和签名)是认证的精华
- 种子是不可预测性的精华
| 压缩前 | 压缩后 | |||
|---|---|---|---|---|
| 对称密码 | 明文 | ---> | 密钥 | 机密性的压缩 |
| 公钥密码 | 明文 | ---> | 密钥 | 机密性的压缩 |
| 单向单列函数 | 消息 | ---> | 散列值 | 完整性的压缩 |
| 消息认证码 | 消息 | ---> | 认证符号(MAC 值) | 认证的压缩 |
| 数字签名 | 消息 | ---> | 认证符号(签名) | 认证的压缩 |
| 伪随机数生成器 | 伪随机数列 | ---> | 种子 | 不可预测性的压缩 |
十、信息安全常识
- 不要使用保密的密码算法
- 使用低强度的密码比不进行任何加密更加危险
- 任何密码总有一天都会被破解
- 密码只是信息安全的一部分
十一、历史上的著名密码
历史上著名的密码有,凯撒密码,简单替换密码,Enigma。
凯撒密码是把明文简单的平移 n 位,得到密文。这种密码强度低,可以用暴力破解它,左右移动尝试 0-25 次就可以破译。
简单替换密码是把明文按照映射表,把明文映射成密文。这种密码也可以破译,利用频率分析即可破译。一篇文章的字母出现的频次基本是固定的,通过观察密文的字母出现频次,可以推断出映射表。
Enigma 是二战中德国使用的密码机器。通过转子和接线的方式来产生密钥。过程略复杂。图灵在 1940 年研究出了破译 Enigma 的机器。
十二、PGP 软件
1. 加密
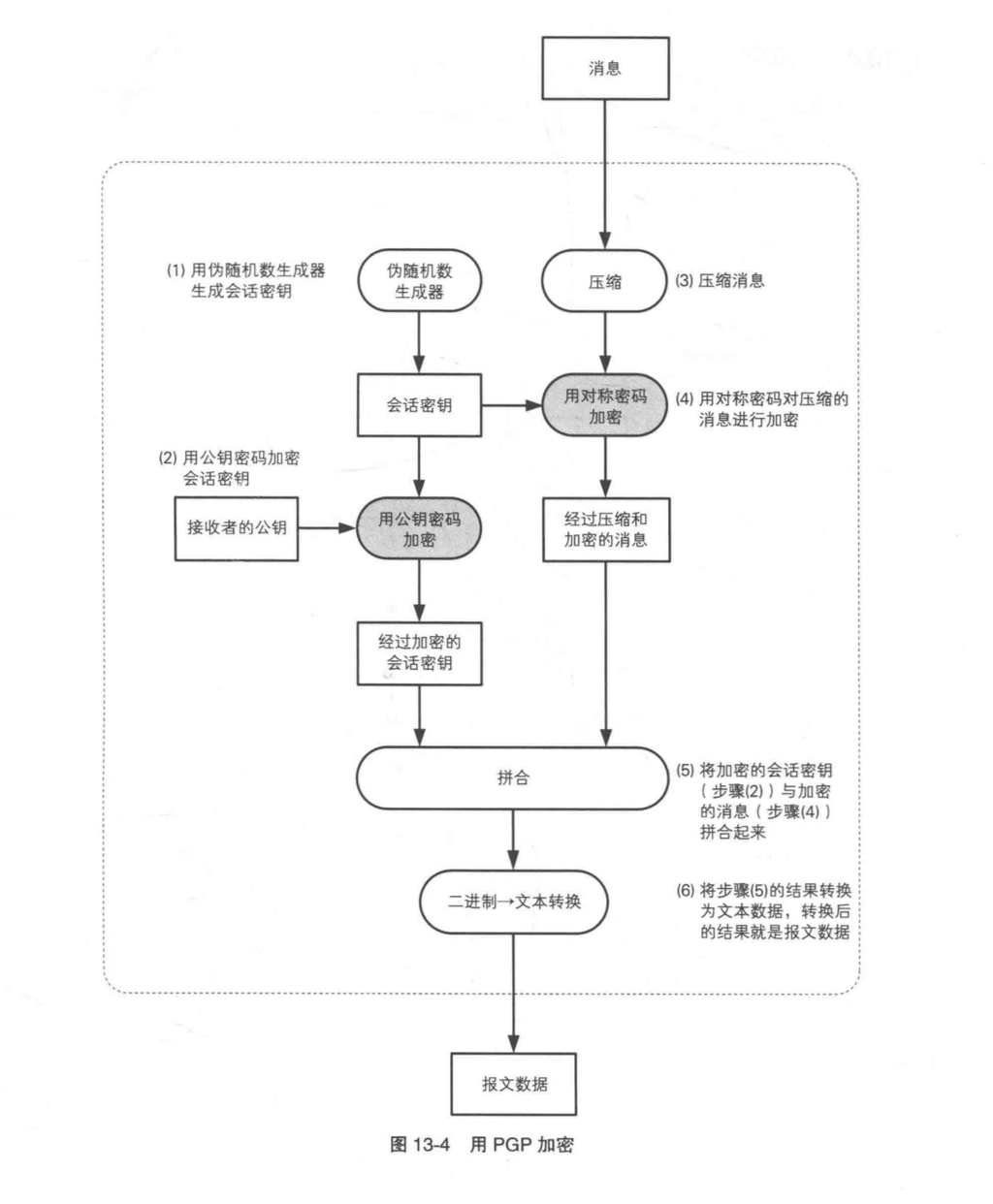
生成和加密会话密钥
- 用伪随机数生成器生成会话密钥。
- 用公钥密码加密会话密钥,这里使用的的密钥是接收者的公钥。
压缩和加密消息
- 压缩消息
- 用对称密码对压缩消息进行加密,这里的密钥使用的是步骤 1 中的会话密钥
- 将第 2 步的加密的会话密钥和第 4 步的加密消息拼在一起
- 将第 5 步的结果转换为文本数据,转换后的结果就是报文数据
用公钥密码加密会话密钥,用对称密码加密消息。
2. 解密
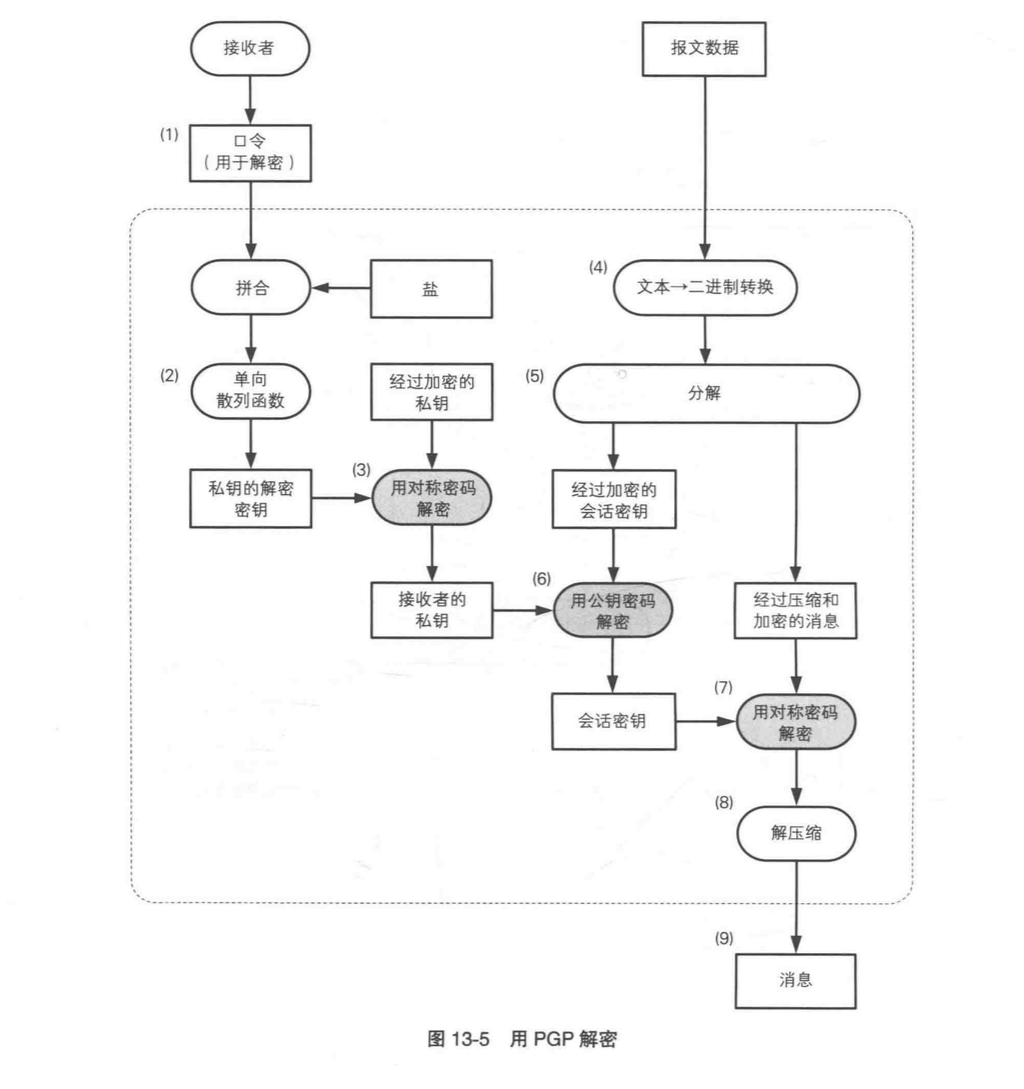
解密私钥
- 接收者输入解密口令,解除口令密码(PBE)
- 求出口令的散列值,生成用于解密私钥的密钥
- 将钥匙串经过加密的私钥进行解密
解密会话密钥
- 将报文数据(文本数据)转换成二进制数据
- 将二进制数据分解成两部分:加密的会话密钥、经过压缩和加密的消息
- 用公钥密码解密会话密钥,这里是用步骤 3 中生成的接收者的私钥
解压和解压缩消息
- 对步骤 5 中得到经过压缩和加密的消息用对称密码进行解密。使用步骤 6 中生成的会话密钥
- 对步骤 7 中得到的经过压缩的消息进行解压缩
- 得到最原始的消息
3. 生成数字签名
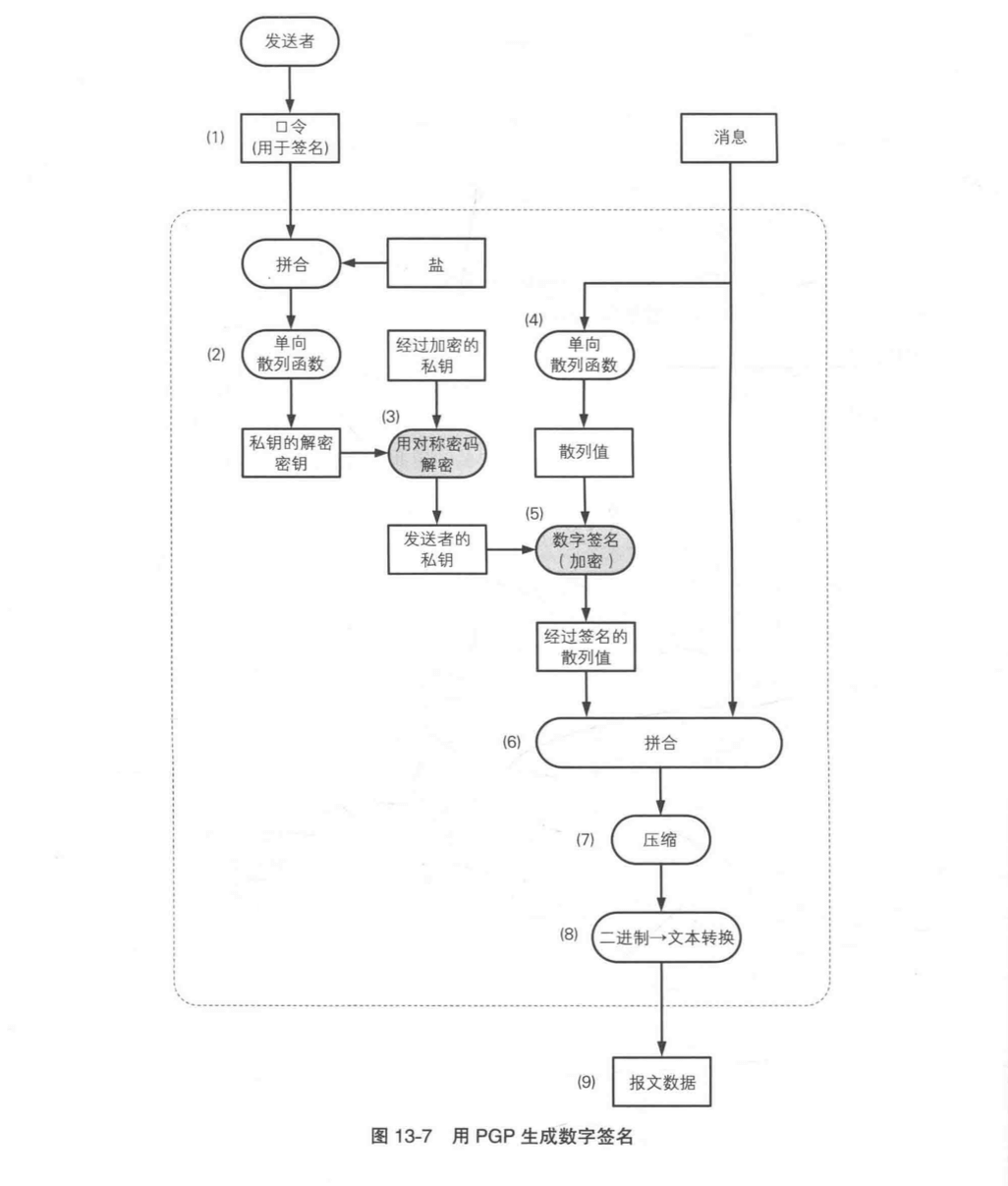
解密私钥
- 发送者输入签名用的口令(PBE)
- 求出口令的散列值,生成用于解密私钥的密钥
- 将钥匙串经过加密的私钥进行解密
生成数字签名
- 用单向散列函数计算消息的散列值
- 对步骤 4 中得到的散列值进行签名,这一步相当于对步骤 3 中得到的私钥进行加密。
- 将步骤 5 中生成的数字签名和消息进行拼合
- 将步骤 6 中的结果进行压缩
- 将步骤 7 的结果转换为文本数据
- 步骤 8 的结果就是报文数据
4. 验证数字签名
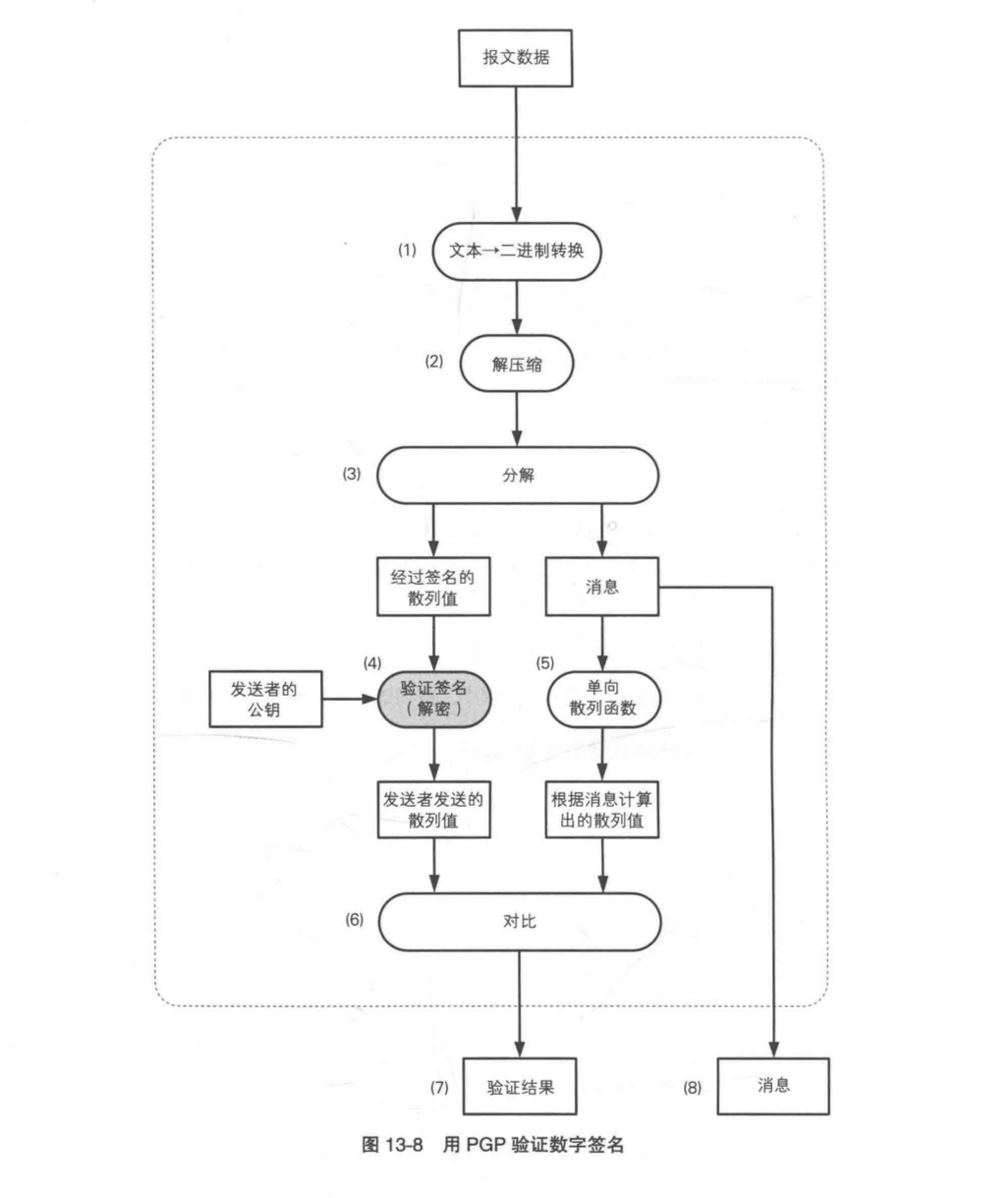
恢复发送者发送的散列值
- 将报文数据(文本数据)转换为二进制数据
- 对经过压缩的数据进行解压缩
- 将解压缩以后的数据分解成经过签名的散列值和消息两部分
- 将经过签名的散列值(经过加密的散列值)用发送者的公钥进行解密,恢复出发送者发送的散列值
对比散列值
- 将步骤 3 中分解出的消息输入单向散列函数进行计算散列值
- 将步骤 4 中得到的散列值与步骤 5 中得到的散列值进行对比
- 如果步骤 6 中结果相等则数字签名验证成功,不相等则验证失败。
- 步骤 3 中分解出的消息就是发送者发送的消息
5. 生成数字签名并加密
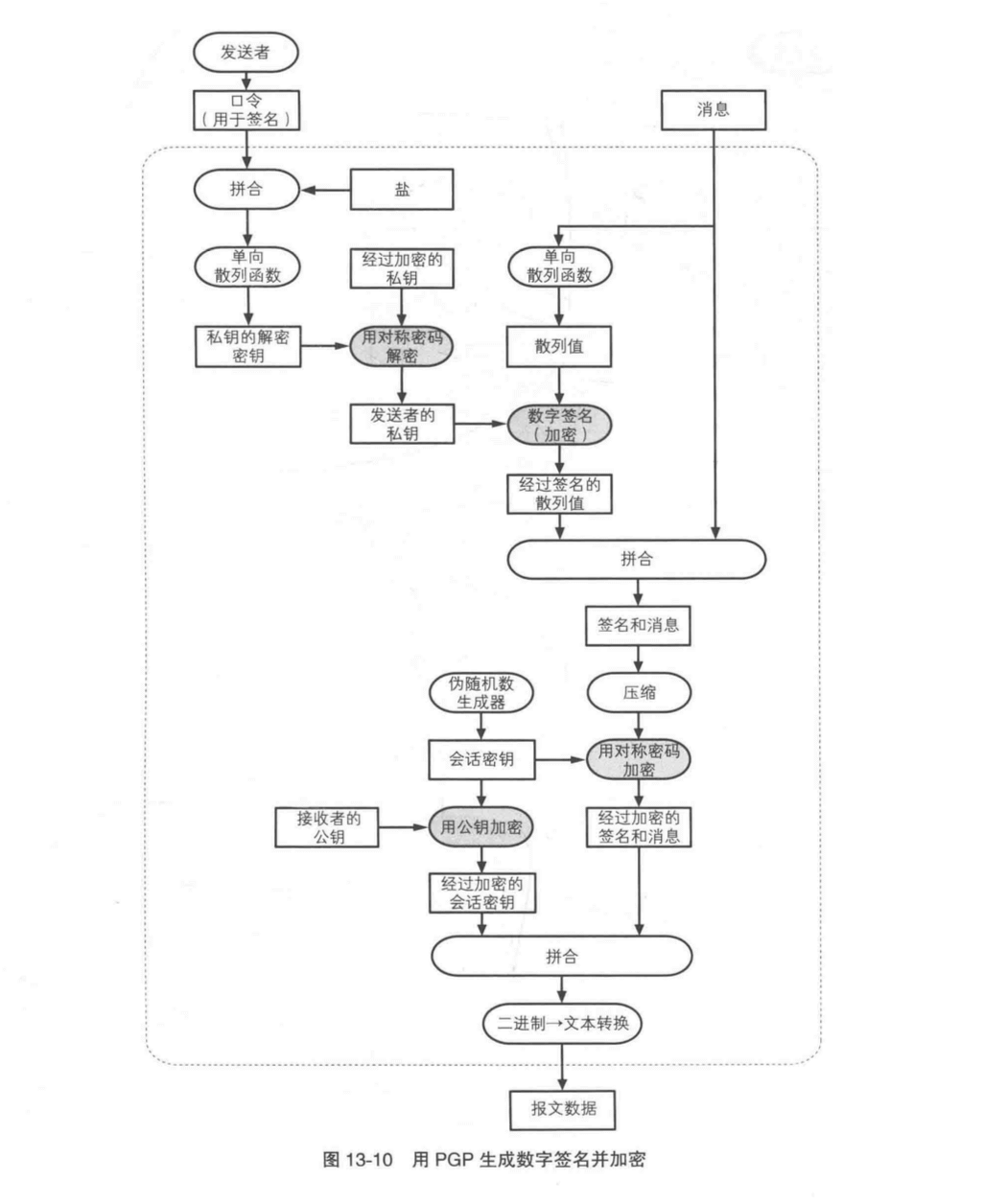
这里看似复杂,其实就是前面几步的组合。先生成数字签名,然后再进行加密。加密的本体不仅仅是消息本身,而是数字签名和消息拼合之后的数据。
6. 解密并验证数字签名
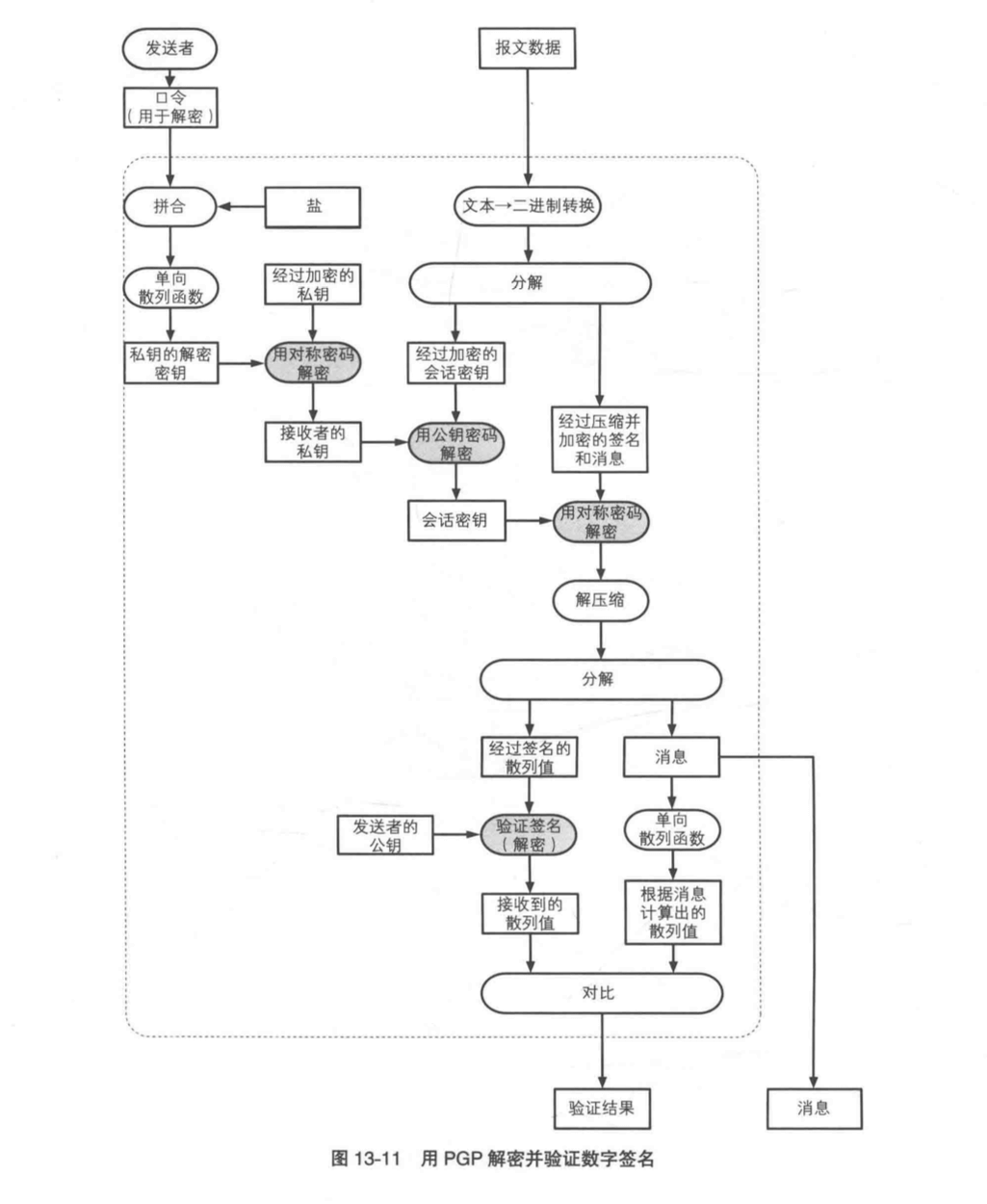
这里也是之前验证数字签名和解密步骤的组合。解密先解密的不仅仅是消息,而是数字签名和消息拼合之后的数据。
Reference:
《图解密码技术》
GitHub Repo:Halfrost-Field
Follow: halfrost · GitHub





