一. Cost Function and Backpropagation
1. Cost Function
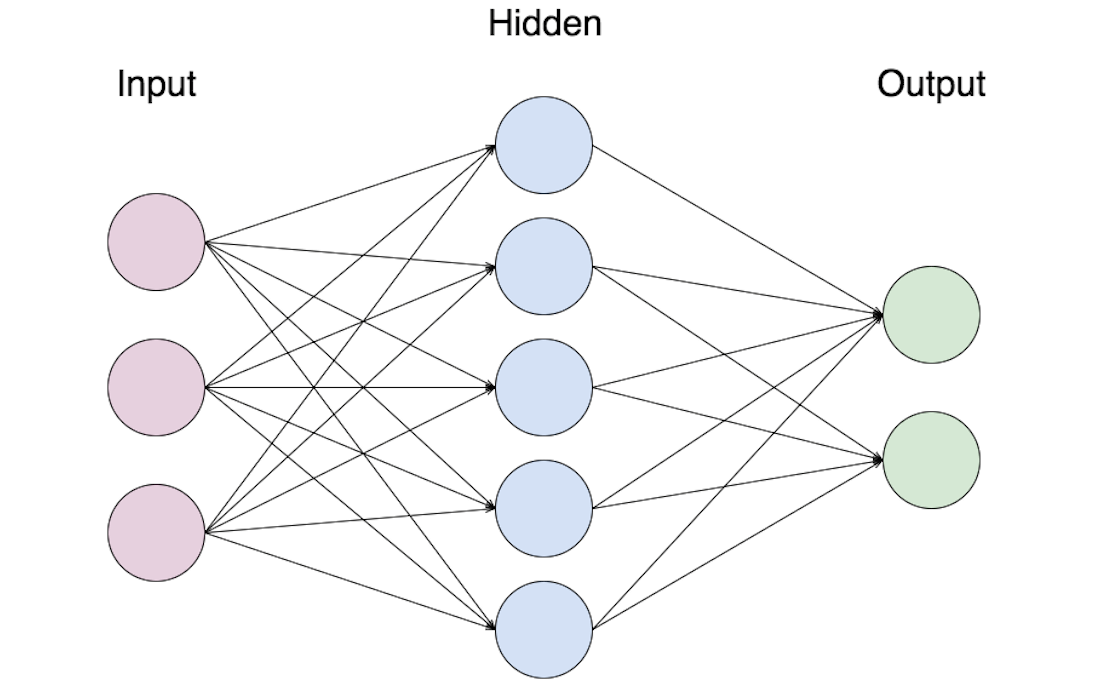
假设训练集中有 m 个训练样本,$\begin{Bmatrix} (x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}), \cdots ,(x^{(m)},y^{(m)}) \end{Bmatrix}$,L 表示神经网络的总层数 Layer,用 $S_{l}$ 表示第 L 层的单元数(神经元的数量),但是不包括第 L 层的偏差单元(常数项)。令 K 为输出层的单元数目,即 最后一层的单元数。
符号约定:
$z_i^{(j)}$ = 第 $j$ 层的第 $i$ 个节点(神经元)的“计算值”
$a_i^{(j)}$ = 第 $j$ 层的第 $i$ 个节点(神经元)的“激活值”
$\Theta^{(l)}_{i,j}$ = 映射第 $l$ 层到第 $l+1$ 层的权值矩阵的第 $i$ 行第 $j$ 列的分量
$L$ = 神经网络总层数(包括输入层、隐层和输出层)
$s_l$ = 第 $l$ 层节点(神经元)个数,不包括偏移量节点。
$K$ = 输出节点个数
$h_{\theta}(x)_k$ = 第 $k$ 个预测输出结果
$x^{(i)}$ = 第 $i$ 个样本特征向量
$x^{(i)}_k$ = 第 $i$ 个样本的第 $k$ 个特征值
$y^{(i)}$ = 第 $i$ 个样本实际结果向量
$y^{(i)}_k$ = 第 $i$ 个样本结果向量的第 $k$ 个分量
之前讨论的逻辑回归中代价函数如下:
$$
\begin{align*}
\rm{CostFunction} = \rm{F}({\theta}) &= -\frac{1}{m}\left [ \sum_{i=1}^{m} y^{(i)}logh_{\theta}(x^{(i)}) + (1-y^{(i)})log(1-h_{\theta}(x^{(i)})) \right ] +\frac{\lambda}{2m} \sum_{j=1}^{n}\theta_{j}^{2} \\
\end{align*}
$$
扩展到神经网络中:
$$
\begin{align*}
\rm{CostFunction} = \rm{F}({\Theta}) &= -\frac{1}{m}\left [ \sum_{i=1}^{m} \sum_{k=1}^{K} y^{(i)}_{k} log(h_{\Theta}(x^{(i)}))_{k} + (1-y^{(i)}_{k})log(1-(h_{\Theta}(x^{(i)}))_{k}) \right ] +\frac{\lambda}{2m} \sum_{l=1}^{L-1} \sum_{i=1}^{S_{l}}\sum_{j=1}^{S_{l} +1}(\Theta_{j,i}^{(l)})^{2} \\
h_{\Theta}(x) &\in \mathbb{R}^{K} \;\;\;\;\;\;\;\;\; (h_{\Theta}(x))_{i} = i^{th} \;\;output \\
\end{align*}
$$
$h_{\Theta}(x)$ 是一个 K 维向量,$ i $ 表示选择输出神经网络输出向量中的第 i 个元素。
神经网络的代价函数相比逻辑回归的代价函数,前一项的求和过程中多了一个 $ \sum_{k=1}^{K} $ ,由于 K 代表了最后一层的单元数,所以这里就是累加了 k 个输出层的代价函数。
后一项是正则化项,神经网络的正则化项看起来特别复杂,其实就是对 $ (\Theta_{j,i}^{(l)})^{2} $ 项对所有的 i,j,l的值求和。正如在逻辑回归中的一样,这里要除去那些对应于偏差值的项,因为我们不对它们进行求和,即不对 $ (\Theta_{j,0}^{(l)})^{2} \;\;\;\;(i=0) $ 项求和。
2. Backpropagation Algorithm 反向传播算法
令 $ \delta_{j}^{(l)} $ 表示第 $l$ 层第 $j$ 个结点的误差。
反向传播从最后一层开始往前推:
$$
\begin{align*}
\delta_{j}^{(L)} &= a_{j}^{(L)} - y_{j} \\
&=(h_{\theta}(x))_{j} - y_{j} \\
\end{align*}
$$
往前计算几步:
$$
\begin{align*}
\delta^{(3)} &= (\Theta^{(3)})^{T}\delta^{(4)} . * g^{'}(z^{(3)}) \\
\delta^{(2)} &= (\Theta^{(2)})^{T}\delta^{(3)} . * g^{'}(z^{(2)}) \\
\end{align*}
$$
逻辑函数(Sigmoid函数)求导:
$$
\begin{align*}
\sigma(x)'&=\left(\frac{1}{1+e^{-x}}\right)'=\frac{-(1+e^{-x})'}{(1+e^{-x})^2}=\frac{-1'-(e^{-x})'}{(1+e^{-x})^2}=\frac{0-(-x)'(e^{-x})}{(1+e^{-x})^2}=\frac{-(-1)(e^{-x})}{(1+e^{-x})^2}=\frac{e^{-x}}{(1+e^{-x})^2} \newline &=\left(\frac{1}{1+e^{-x}}\right)\left(\frac{e^{-x}}{1+e^{-x}}\right)=\sigma(x)\left(\frac{+1-1 + e^{-x}}{1+e^{-x}}\right)=\sigma(x)\left(\frac{1 + e^{-x}}{1+e^{-x}} - \frac{1}{1+e^{-x}}\right)\\
&=\sigma(x)(1 - \sigma(x))\\
\end{align*}
$$
可以算出 $g^{'}(z^{(3)}) = a^{(3)} . * (1-a^{(3)})$ , $g^{'}(z^{(2)}) = a^{(2)} . * (1-a^{(2)})$。

于是可以给出反向传播的算法步骤:
首先有一个训练集 $\begin{Bmatrix} (x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}), \cdots ,(x^{(m)},y^{(m)}) \end{Bmatrix}$,初始值对每一个 $(l,i,j)$ 都设置 $\Delta^{(l)}_{i,j} := 0$ ,即初始矩阵是全零矩阵。
针对 $1-m$ 训练集开始以下步骤的训练:
(1) 前向传播
设置 $ a^{(1)} := x^{(t)} $,并按照前向传播的方法,计算出每一层的激励 $a^{(l)}$ 。
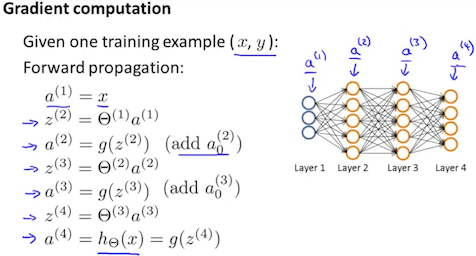
(2) 计算误差
利用 $y^{(t)}$,计算 $\delta^{(L)} = a^{(L)} - y^{t}$
其中 $L$ 是我们的总层数,$a^{(L)}$ 是最后一层激活单元输出的向量。所以我们最后一层的“误差值”仅仅是我们在最后一层的实际结果和 y 中的正确输出的差异。为了获得最后一层之前的图层的增量值,我们可以使用下面步骤中的方程,让我们从右向左前进:
(3) 反向传播
通过 $\delta^{(l)} = ((\Theta^{(l)})^{(T)}\delta^{(l+1)}).* a^{(l)} .*(1-a^{(l)})$,计算 $\delta^{(L-1)},\delta^{(L-2)},\cdots,\delta^{(2)}$ 计算出每一层神经节点的误差。
(4) 计算偏导数
最后利用 $\Delta^{(l)}_{i,j} := \Delta^{(l)}_{i,j} + a_{j}^{(l)}\delta_{i}^{(l+1)}$,或者矢量表示为 $\Delta^{(l)} := \Delta^{(l)} + \delta^{(l+1)}(a^{(l)})^{T}$。
$$
\frac{\partial }{\partial \Theta_{i,j}^{(l)} }F(\Theta) = D_{i,j}^{(l)} := \left\{\begin{matrix}
\frac{1}{m} \left( \Delta_{i,j}^{(l)} + \lambda\Theta_{i,j}^{(l)} \right) \;\;\;\;\;\;\;\; j\neq 0\\
\frac{1}{m}\Delta_{i,j}^{(l)} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; j = 0
\end{matrix}\right.$$
(5) 更新矩阵
更新各层的权值矩阵 $\Theta^{(l)}$ ,其中 $\alpha$ 为学习率:
$$\Theta^{(l)} = \Theta^{(l)} - \alpha D^{(l)}$$
二. 推导
1. 目标
求 $\min_\Theta F(\Theta)$
2. 思路
类似梯度下降法,给定一个初值后,计算出所有节点的计算值和激活值,然后根据代价函数的变化不断调整参数值(权值),最终不断逼近最优结果,使代价函数值最小。
3. 推导过程
为了实现上述思路,我们必须首先计算代价函数的偏导数:
$$\dfrac{\partial}{\partial \Theta_{i,j}^{(l)}}F(\Theta)$$
这个偏导并不好求,为了方便推导,我们假设只有一个样本($m=1$,可忽略代价函数中的外部求和),并舍弃正规化部分,然后分为两种情况来求。
情况1 隐藏层 → 输出层
我们知道:
$$
\begin{align*}
h_\Theta(x) &= a^{(j+1)} = g(z^{(j+1)}) \\
z^{(j)} &= \Theta^{(j-1)}a^{(j-1)} \\
\end{align*}
$$
另外,输出层即第$L$层。
所以:
$$\dfrac{\partial}{\partial \Theta_{i,j}^{(L)}}F(\Theta)
= \dfrac{\partial F(\Theta)}{\partial h_{\Theta}(x)_i} \dfrac{\partial h_{\Theta}(x)_i}{\partial z_i^{(L)}} \dfrac{\partial z_i^{(L)}}{\partial \Theta_{i,j}^{(L)}}
= \dfrac{\partial F(\Theta)}{\partial a_i^{(L)}} \dfrac{\partial a_i^{(L)}}{\partial z_i^{(L)}} \dfrac{\partial z_i^{(L)}}{\partial \Theta_{i,j}^{(L)}}$$
其中:
$$
\begin{align*}
\dfrac{\partial F(\Theta)}{\partial a_i^{(L)}} &= \dfrac{a_i^{(L)} - y_i}{(1 - a_i^{(L)})a_i^{(L)}} \\
\dfrac{\partial a_i^{(L)}}{\partial z_i^{(L)}} &= \dfrac{\partial g(z_i^{(L)})}{\partial z_i^{(L)}} = \dfrac{e^{z_i^{(L)}}}{(e^{z_i^{(L)}}+1)^2} = a_i^{(L)} (1 - a_i^{(L)}) \\
\dfrac{\partial z_i^{(L)}}{\partial \Theta_{i,j}^{(L)}} &= \dfrac{\partial ( \sum_{k=0}^{s_{(L-1)}}\; \Theta_{i,k}^{(L)} a_k^{(L-1)})}{\partial \Theta_{i,j}^{(L)}} = a_j^{(L-1)} \\
\end{align*}
$$
综上:
$$
\begin{split}
\dfrac{\partial}{\partial \Theta_{i,j}^{(L)}}F(\Theta)
=& \dfrac{\partial F(\Theta)}{\partial a_i^{(L)}} \dfrac{\partial a_i^{(L)}}{\partial z_i^{(L)}} \dfrac{\partial z_i^{(L)}}{\partial \Theta_{i,j}^{(L)}} \newline
=& \dfrac{a_i^{(L)} - y_i}{(1 - a_i^{(L)})a_i^{(L)}} a_i^{(L)} (1 - a_i^{(L)}) a_j^{(L-1)} \newline
=& (a_i^{(L)} - y_i)a_j^{(L-1)}
\end{split}
$$
情况2 隐藏层 / 输入层 → 隐藏层
因为 $a^{(1)}=x$,所以可以将输入层和隐藏层同样对待。
$$\dfrac{\partial}{\partial \Theta_{i,j}^{(l)}}F(\Theta)
=\dfrac{\partial F(\Theta)}{\partial a_i^{(l)}} \dfrac{\partial a_i^{(l)}}{\partial z_i^{(l)}} \dfrac{\partial z_i^{(l)}}{\partial \Theta_{i,j}^{(l)}}\ (l = 1, 2, ..., L-1)$$
其中后两部分偏导很容易根据前面所得类推出来:
$$
\begin{align*}
\dfrac{\partial a_i^{(l)}}{\partial z_i^{(l)}} &= \dfrac{e^{z_i^{(l)}}}{(e^{z_i^{(l)}}+1)^2} = a_i^{(l)} (1 - a_i^{(l)}) \\
\dfrac{\partial z_i^{(l)}}{\partial \Theta_{i,j}^{(l)}} &= a_j^{(l-1)} \\
\end{align*}
$$
第一部分偏导是不好求解的,或者说是没法直接求解的,我们可以得到一个递推式:
$$\dfrac{\partial F(\Theta)}{\partial a_i^{(l)}}
= \sum_{k=1}^{s_{(l+1)}} \Bigg[\dfrac{\partial F(\Theta)}{\partial a_k^{(l+1)}} \dfrac{\partial a_k^{(l+1)}}{\partial z_k^{(l+1)}} \dfrac{\partial z_k^{(l+1)}}{\partial a_i^{(l)}}\Bigg]$$
因为该层的激活值与下一层各节点都有关,链式法则求导时需一一求导,所以有上式中的求和。
递推式中第一部分是递推项,后两部分同样易求:
$$
\begin{align*}
\dfrac{\partial a_k^{(l+1)}}{\partial z_{k}^{(l+1)}} &= \dfrac{e^{z_{k}^{(l+1)}}}{(e^{z_{k}^{(l+1)}}+1)^2} = a_k^{(l+1)} (1 - a_k^{(l+1)}) \\
\dfrac{\partial z_k^{(l+1)}}{\partial a_i^{(l)}} &= \dfrac{\partial ( \sum_{j=0}^{s_l} \Theta_{k,j}^{(l+1)} a_j^{(l)})}{\partial a_i^{(l)}} = \Theta_{k,i}^{(l+1)} \\
\end{align*}
$$
所以,递推式为:
$$
\begin{split}
\dfrac{\partial F(\Theta)}{\partial a_i^{(l)}}
=& \sum_{k=1}^{s_{(l+1)}} \Bigg[\dfrac{\partial F(\Theta)}{\partial a_k^{(l+1)}} \dfrac{\partial a_k^{(l+1)}}{\partial z_k^{(l+1)}} \dfrac{\partial z_k^{(l+1)}}{\partial a_i^{(l)}}\Bigg] \newline
=& \sum_{k=1}^{s_{(l+1)}} \Bigg[ \dfrac{\partial F(\Theta)}{\partial a_k^{(l+1)}} \dfrac{\partial a_k^{(l+1)}}{\partial z_k^{(l+1)}} \Theta_{k,i}^{(l+1)} \Bigg] \newline
=& \sum_{k=1}^{s_{(l+1)}} \Bigg[ \dfrac{\partial F(\Theta)}{\partial a_k^{(l+1)}} a_k^{(l+1)} (1 - a_k^{(l+1)}) \Theta_{k,i}^{(l+1)} \Bigg]
\end{split}
$$
为了简化表达式,定义第 $l$ 层第 $i$ 个节点的误差:
$$\begin{split}
\delta^{(l)}_i
=& \dfrac{\partial F(\Theta)}{\partial a_i^{(l)}} \dfrac{\partial a_i^{(l)}}{\partial z_i^{(l)}} \newline
=& \dfrac{\partial F(\Theta)}{\partial a_i^{(l)}} a_i^{(l)} (1 - a_i^{(l)}) \newline
=& \sum_{k=1}^{s_{(l+1)}} \Bigg[ \dfrac{\partial F(\Theta)}{\partial a_k^{(l+1)}} \dfrac{\partial a_k^{(l+1)}}{\partial z_k^{(l+1)}} \Theta_{k,i}^{(l+1)} \Bigg] a_i^{(l)} (1 - a_i^{(l)}) \newline
=& \sum_{k=1}^{s_{(l+1)}} \Big[\delta^{(l+1)}_k \Theta_{k,i}^{(l+1)} \Big] a_i^{(l)} (1 - a_i^{(l)})
\end{split}$$
可知,情况1的误差为:
$$\begin{split}
\delta^{(L)}_i
=& \dfrac{\partial F(\Theta)}{\partial a_i^{(L)}} \dfrac{\partial a_i^{(L)}}{\partial z_i^{(L)}} \newline
=& \dfrac{a_i^{(L)} - y_i}{(1 - a_i^{(L)})a_i^{(L)}} a_i^{(L)} (1 - a_i^{(L)}) \newline
=& a_i^{(L)} - y_i
\end{split}$$
最终的代价函数的偏导为:
$$\begin{split}
\dfrac{\partial}{\partial \Theta_{i,j}^{(l)}}F(\Theta)
=& \dfrac{\partial F(\Theta)}{\partial a_i^{(l)}} \dfrac{\partial a_i^{(l)}}{\partial z_i^{(l)}} \dfrac{\partial z_i^{(l)}}{\partial \Theta_{i,j}^{(l)}} \newline
=& \delta^{(l)}_i \dfrac{\partial z_i^{(l)}}{\partial \Theta_{i,j}^{(l)}} \newline
=& \delta^{(l)}_i a_j^{(l-1)}
\end{split}$$
我们发现,引入误差 $\delta^{(l)}_i$ 后,这个公式可以通用于情况1和情况2。
可以看出,当前层的代价函数偏导,需要依赖于后一层的计算结果。这也是为什么这个算法的名称叫做“反向传播算法”。
4. 总结算法公式
$$\delta^{(L)}_i = a_i^{(L)} - y_i$$
$$\delta^{(l)}_i = \sum_{k=1}^{s_{(l+1)}} \Big[\delta^{(l+1)}_k \Theta_{k,i}^{(l+1)} \Big] a_i^{(l)} (1 - a_i^{(l)})$$
$$\dfrac{\partial}{\partial \Theta_{i,j}^{(l)}}F(\Theta) = \delta^{(l)}_i a_j^{(l-1)}$$
三. Backpropagation Algorithm 反向传播算法过程
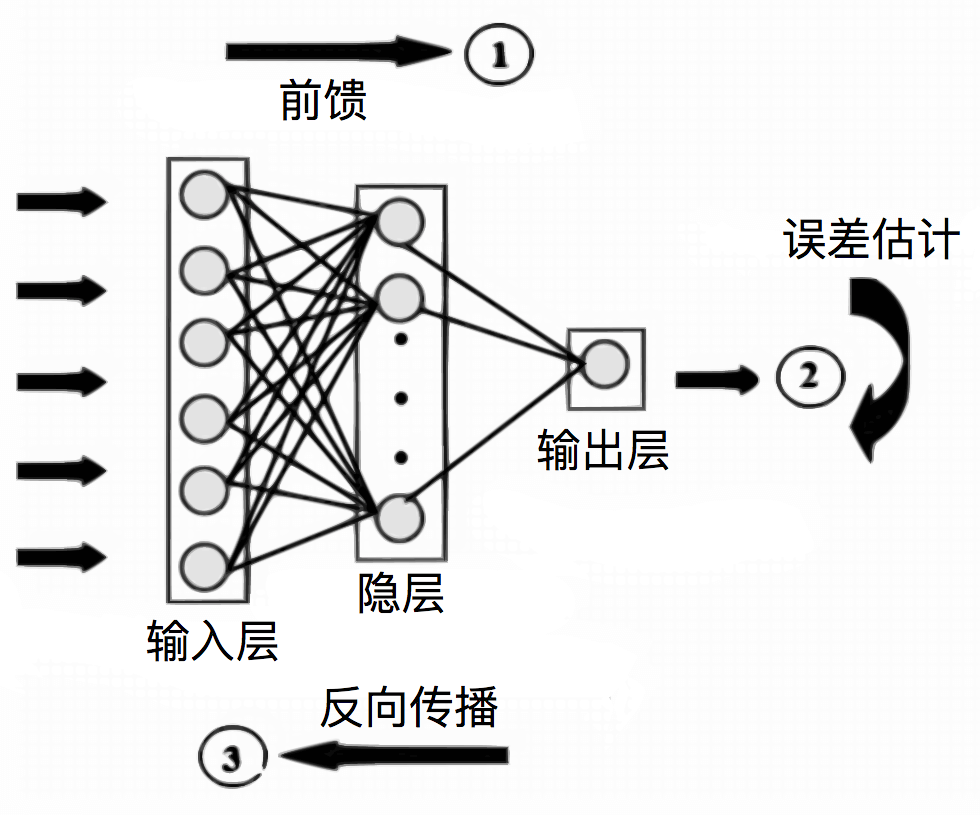
有了上述推导,我们描述一下算法具体的操作流程:
- 输入:输入样本数据,初始化权值参数(建议随机生成较小的数)。
- 前馈:计算各层($l=2, 3, ..., L$)各节点的计算值($z^{(l)}=\Theta^{(l-1)}a^{(l-1)}$)和激活值($a^{(l)}=g(z^{(l)})$)。
- 输出层误差:计算输出层误差(公式见前文)。
- 反向传播误差:计算各层($l=L-1, L-2, ..., 2$)的误差 $\delta^{(l)}$(公式见前文)。
- 输出:得到代价函数的梯度 $\nabla F(\Theta)$(参考前文偏导计算公式)。
反向传播算法帮助我们得到了代价函数的梯度,我们就可以借助梯度下降法训练神经网络了。
$$\Theta := \Theta - \alpha \nabla F(\Theta)$$
$\alpha $ 为学习速率。
四. Backpropagation Algorithm implementation 算法实现
以3层神经网络(输入层、隐层、输出层各一)为例。
- X 为大小为样本数∗特征数的样本特征矩阵
- Y 为大小为样本数∗输出节点数的样本类别(结果)矩阵
- Theta1 为输入层→隐层的权值矩阵
- Theta2 为隐藏层→输出层的权值矩阵
- m 为样本数
- K 为输出层节点数
- H 为隐藏层节点数
- sigmoid 函数即逻辑函数(S型函数,Sigmoid函数)
- sigmoidGradient 函数即 Sigmoid 函数的导函数
- 代码实现中,考虑了正规化,避免出现过拟合问题。
1. 前馈阶段
逐层计算各节点值和激活值。
a1 = X;
z2 = [ones(m, 1), a1] * Theta1';
a2 = sigmoid(z2);
z3 = [ones(m, 1), a2] * Theta2';
a3 = sigmoid(z3);
2. 代价函数
正规化部分需注意代价函数不惩罚偏移参数,即 $\Theta_{i,0}$(代码表示为 $Theta(:,1)$)。
F = 1 / m * sum((-log(a3) .* Y - log(1 .- a3) .* (1 - Y))(:)) + ... # 代价部分
lambda / 2 / m * (sum((Theta1(:, 2:end) .^ 2)(:)) + sum((Theta2(:, 2:end) .^ 2)(:)));
# 正规化部分,lambda为正规参数,需除去偏移参数Theta*(:,1)
3. 反向传播
输出层误差和 $\Theta^{(2)}$ 梯度计算,反向传播计算隐层误差和 $\Theta^{(1)}$ 梯度。
仍需注意正规化时排除偏移参数,另外注意为激活值补一个偏移量 $1$。
function g = sigmoid(z)
g = 1.0 ./ (1.0 + exp(-z));
end
function g = sigmoidGradient(z)
g = sigmoid(z) .* (1 - sigmoid(z));
end
delta3 = a3 - Y;
Theta2_grad = 1 / m * delta3' * [ones(m, 1), a2] + ...
lambda / m * [zeros(K, 1), Theta2(:, 2:end)]; # 正规化部分
delta2 = (delta3 * Theta2 .* sigmoidGradient([ones(m, 1), z2]));
delta2 = delta2(:, 2:end); # 反向计算多一个偏移参数误差,除去
Theta1_grad = 1 / m * delta2' * [ones(m, 1), a1] + ...
lambda / m * [zeros(H, 1), Theta1(:, 2:end)]; # 正规化部分
推荐阅读:
Principles of training multi-layer neural network using backpropagation
如何直观地解释 back propagation 算法?
GitHub Repo:Halfrost-Field
Follow: halfrost · GitHub
Source: https://github.com/halfrost/Halfrost-Field/blob/master/contents/Machine_Learning/Neural_Networks_Learning.ipynb










